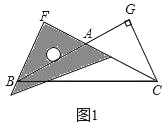
【题目】在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
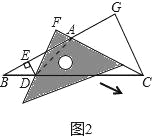
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
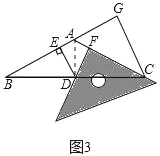
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,若AG:AB=5:13,BC=4![]() ,求DE+DF的值.
,求DE+DF的值.

参考答案:
【答案】(1)BF=CG,理由详见解析;(2)DF+DE=CG,理由详见解析;(3)8.
【解析】【试题分析】(1)如图1,BF和CG可看成△ABC的高,根据S△ABC=![]() ACBF=
ACBF=![]() ABCG,AB=AC,即可解决问题;
ABCG,AB=AC,即可解决问题;
(2)连接AD,如图2.由于DF⊥AC,DE⊥AB,CG⊥AB,因此DF、DE、CG可分别看成△ACD、△ABD、△ABC的高,再根据S△ACD+S△ABD=S△ABC,AB=AC,即可解决问题;
(3)连接AD,如图3.,同(2)可得:DF+DE=CG.设AG=5x,根据条件可得AC=AB=13x,运用勾股定理可得GC=12x,然后在Rt△BGC中运用勾股定理即可求出x的值,从而解决问题.
【试题解析】
(1)猜想:BF=CG.
理由:如图1.
∵BF⊥AC,CG⊥AB,
∴S△ABC=![]() ACBF=
ACBF=![]() ABCG.
ABCG.
∵AB=AC,
∴BF=CG;
(2)猜想:DE+DF=CG.
理由:连接AD,如图2.
∵DF⊥AC,DE⊥AB,CG⊥AB,
∴S△ACD=![]() ACDF,S△ABD=
ACDF,S△ABD=![]() ABDE,S△ABC=
ABDE,S△ABC=![]() ABCG.
ABCG.
∵S△ACD+S△ABD=S△ABC,
∴![]() ACDF+
ACDF+![]() ABDE=
ABDE=![]() ABCG.
ABCG.
∵AB=AC,
∴DF+DE=CG;
(3)连接AD,如图3.
同(2)可得:DF+DE=CG.
设AG=5x,
∵AG:AB=5:13,AB=AC,
∴AC=AB=13x.
∴∠G=90°,
∴GC=![]() =12x.
=12x.
在Rt△BGC中,
∵BG=AB+AG=13x+5x=18x,GC=12x,BC=4![]() ,
,
∴(18x)2+(12x)2=(4![]() )2,
)2,
解得:x=![]() ,
,
∴DE+DF=CG=12x=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b满足
 ,
, ,且有理数a、b、c在数轴上对应的点分别为A、B、C.
,且有理数a、b、c在数轴上对应的点分别为A、B、C. 则
则 ______,
______, ______,
______, ______.
______. 点D是数轴上A点右侧一动点,点E、点F分别为CD、AD中点,当点D运动时,线段EF的长度是否发生变化,若变化,请说明理由,若不变,请求出其值;
点D是数轴上A点右侧一动点,点E、点F分别为CD、AD中点,当点D运动时,线段EF的长度是否发生变化,若变化,请说明理由,若不变,请求出其值; 若点A、B、C在数轴上运动,其中点C以每秒1个单位的速度向左运动,同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动
若点A、B、C在数轴上运动,其中点C以每秒1个单位的速度向左运动,同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动 请问:是否存在一个常数m使得
请问:是否存在一个常数m使得 不随运动时间t的改变而改变
不随运动时间t的改变而改变 若存在,请求出m和这个不变化的值;若不存在,请说明理由.
若存在,请求出m和这个不变化的值;若不存在,请说明理由.

-
科目: 来源: 题型:
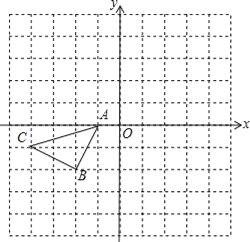
查看答案和解析>>【题目】如图的正方形格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△AB1C1.若△ABC内有一点P(a,b),则经过两次变换后点P的坐标变为 .
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)若将△ABC绕某点逆时针旋转90°后,其对应点分别为A3(2,1),B3(4,0),C3(3,﹣2),则旋转中心坐标为 .
-
科目: 来源: 题型:
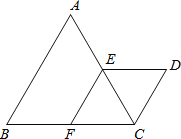
查看答案和解析>>【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别为AC、BC的中点。
(1) 求证:四边形EFCD是菱形;(2)如果AB=10,求D、F两点间的距离。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组.
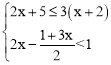 把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.

相关试题

