【题目】在平面直角坐标系xOy中,已知△ABC三个顶点的坐标分别为A(-2,0),B(-4,4),C(3,-3).
(1)画出△ABC;
(2)画出△ABC向右平移3个单位长度,再向上平移4个单位长度后得到的△A1B1C1;
(3)求出△A1B1C1的面积.

参考答案:
【答案】(1)详见解析;(2)详见解析;(3)7
【解析】
(1)根据A,B,C三点坐标描出各点,顺次连接各点即可;
(2)根据图形平移的性质先画出三个对应顶点A1,B1,C1,再顺次连接即可得到△A1B1C1;
(3)过点B1作x轴的垂线,过点C1作y轴的垂线,两垂线相交于点D,连接A1D,利用割补法即![]() ,可求得△A1B1C1的面积.
,可求得△A1B1C1的面积.
解:(1)△ABC如图所示;
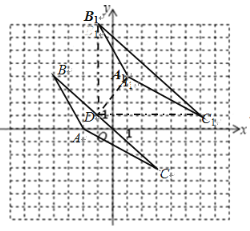
(2)△A1B1C1如图所示;
(3)过点B1作x轴的垂线,过点C1作y轴的垂线,两垂线相交于点D,连接A1D,
∴![]() =
=![]() ×7×7﹣
×7×7﹣![]() ×7×2﹣
×7×2﹣![]() ×7×3=
×7×3=![]() =7.
=7.
故△A1B1C1的面积为7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).
(1)用画树状图或列表等方法求出点(x,y)的所有可能情况;
(2)求点(x,y)在二次函数y=ax2﹣4ax+c(a≠0)图象的对称轴上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.

(1)求BC及阴影部分的面积;
(2)求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列四个条件:① ∠BAC=∠DCA;② ∠DAC=∠BCA;③ ∠ABD=∠CDB;④ ∠ADB=∠CBD,其中能使 AD∥BC的条件是( )

A.①②B.③④C.②④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.求证:∠1=∠2.

证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴ ∠1=∠2( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知 A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式:
 .
.(1)求A,B,C三点的坐标;
(2)如果在第二象限内有一点P(m,
 ),若四边形ABOP的面积与三角形ABC 的面积相等,求点P的坐标.
),若四边形ABOP的面积与三角形ABC 的面积相等,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣2+7﹣(﹣3)﹣2
(2)(﹣4)×5+(﹣120)÷6
(3)9
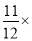 (﹣12)+35.5×4﹣5.5×4
(﹣12)+35.5×4﹣5.5×4(4)﹣22
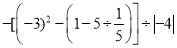
相关试题

