Question

【题目】已知：如图，AB是⊙O的直径，AB=6，点C，D在⊙O上，且CD平分∠ACB，∠CAB=60°．

（1）求BC及阴影部分的面积；
（2）求CD的长．

Answer 1

【答案】
（1）解：∵AB是⊙O的直径，

∴∠ACB=90°．

在Rt△ACB中，

∵∠CAB=60°，AB=6，

∴BC=ABsin∠CAB=6× =3 ，∠CBA=30°，

如图1，连接OC，过点C作CE⊥x轴于点E，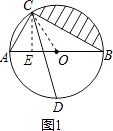

在Rt△BCE中，CE=BCsin∠CBA=3 × ，

阴影部分的面积=S扇形OBC﹣S△OBC= ×π×9﹣ ×3=3π﹣ ；

（2）解：连接AD，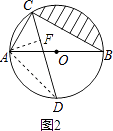

∵∠ABC=30°，

∴∠ADC=∠ABC=30°，

在△CAD中，AC=3，∠ACD=45°，

过点A作AF⊥CD于点F，在Rt△AFC中，AF=CF= ，

在Rt△AFD中，

∵DF= AF= ，

∴CD=CF+FD= + ．

【解析】（1）求阴影弓形的面积用扇形的面积减去三角形的面积。
（2）根据同弦所对的圆周角相等，构建有两个特殊角的三角形。CD平分∠ACB，所以有∠ACD=45°，然后作AF⊥CD，知AC边，求CD。
【考点精析】本题主要考查了圆周角定理和互余两角的三角函数关系的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；互余关系：sinA=cos(90°—A)，cosA=sin(90°—A)，tanA=cot(90°—A)，cotA=tan(90°—A)才能正确解答此题．