【题目】在边长为1的正方形网格图中,点B的坐标为(2,0),点A的坐标为(0,-3).
(1)在图1中,请建立合适的坐标系,把线段AB绕原点旋转180°得线段DE(其中A与D是对应点),则四边形ABDE是 形,面积等于 .
(2)在图2中,仅使用无刻度的直尺,作出以AB为边的矩形ABFG,使其面积为11(保留作图痕迹,不写做法)

参考答案:
【答案】(1)菱形,12;(2)见解析
【解析】
(1)如图1,建立直角坐标系,四边形![]() 是菱形,根据
是菱形,根据![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,可求得菱形
,可求得菱形![]() 的面积.
的面积.
(2)如图2,连接![]() ,
,![]() ,交于点
,交于点![]() ,得
,得![]() 的两条垂线,则得到矩形
的两条垂线,则得到矩形![]() ,由
,由![]() 的值,可得
的值,可得![]() 的值,可得
的值,可得![]() 的值和
的值和![]() 的值,又
的值,又![]() ,则矩形
,则矩形![]() 的面积为:
的面积为:![]() ,既得矩形
,既得矩形![]() 即为所求.
即为所求.
(1)如图1所示,建立直角坐标系,
按照线段![]() 绕原点旋转
绕原点旋转![]() 得线段
得线段![]() ,画出四边形
,画出四边形![]() ,
,
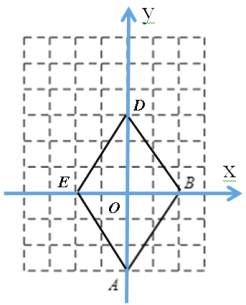
图1
根据图形可得,四边形![]() 是菱形,
是菱形,
∵![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴四边形![]() 的面积为:
的面积为:![]() .
.
故四边形![]() 是菱形,面积等于12.
是菱形,面积等于12.
(2)如图2,连接![]() ,
,![]() ,交于点
,交于点![]() ,
,
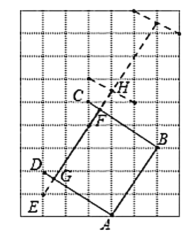
图2
由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
同理可得,![]() ,
,
又![]() ,
,
此时,矩形![]() 的面积为:
的面积为:![]() ,
,
故矩形![]() 即为所求.
即为所求.
-
科目: 来源: 题型:
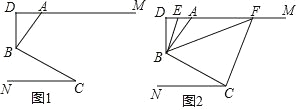
查看答案和解析>>【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD(______________________).
∴∠B=_______(_____________________).
又∵∠B=∠D(已知),
∴∠DCE=∠D(_____________________).
∴AD∥BE(_____________________).
∴∠E=∠DFE(_____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足2x1=|x2|+3,求m的值.
-
科目: 来源: 题型:
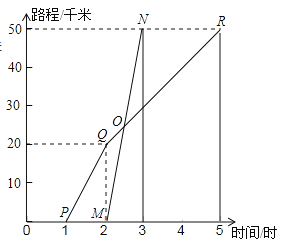
查看答案和解析>>【题目】如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲?
-
科目: 来源: 题型:
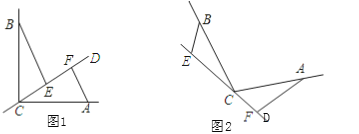
查看答案和解析>>【题目】已知:CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,如图1,若∠BCA=90°,∠α=90°,则BE______CF;并说明理由.
(2)如图2,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:__________.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
相关试题

