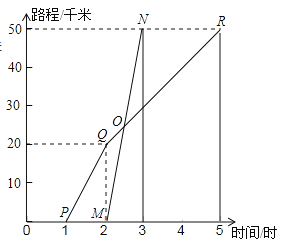
【题目】如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲?
参考答案:
【答案】(1)甲更早,早出发1 h;(2)乙更早,早到2 h;(3)甲的平均速度12.5km/h, 乙的平均速度是50km/h;(4) 乙出发0.5 h就追上甲
【解析】
(1)(2)读图可知;
(3)从图中得:甲和乙所走的路程都是50千米,甲一共用了4小时,乙一共用了1小时,根据速度=![]() ,代入计算得出;
,代入计算得出;
(4)从图中得:甲在走完全程时,前1小时速度为20千米/小时,从第2小时开始,速度为![]() =10千米/小时,因此设乙出发x小时就追上甲,则从图中看,是在甲速度为10千米/小时时与乙相遇,所以甲的路程为20+10x,乙的路程为50x,列方程解出即可.
=10千米/小时,因此设乙出发x小时就追上甲,则从图中看,是在甲速度为10千米/小时时与乙相遇,所以甲的路程为20+10x,乙的路程为50x,列方程解出即可.
(1)甲下午1时出发,乙下午2时出发,所以甲更早,早出发1小时;
(2)甲5时到达,乙3时到达,所以乙更早,早到2小时;
(3)乙的速度=![]() =50(千米/时),甲的平均速度=
=50(千米/时),甲的平均速度=![]() =12.5(千米/时);
=12.5(千米/时);
(4)设乙出发x小时就追上甲,根据题意得:50x=20+10x,x=0.5.
答:乙出发0.5小时就追上甲.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD(______________________).
∴∠B=_______(_____________________).
又∵∠B=∠D(已知),
∴∠DCE=∠D(_____________________).
∴AD∥BE(_____________________).
∴∠E=∠DFE(_____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足2x1=|x2|+3,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的正方形网格图中,点B的坐标为(2,0),点A的坐标为(0,-3).
(1)在图1中,请建立合适的坐标系,把线段AB绕原点旋转180°得线段DE(其中A与D是对应点),则四边形ABDE是 形,面积等于 .
(2)在图2中,仅使用无刻度的直尺,作出以AB为边的矩形ABFG,使其面积为11(保留作图痕迹,不写做法)

-
科目: 来源: 题型:
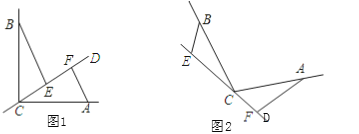
查看答案和解析>>【题目】已知:CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,如图1,若∠BCA=90°,∠α=90°,则BE______CF;并说明理由.
(2)如图2,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想:__________.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文化十大精深,源远流长,我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子短一托。”其大意 为:现有一根竿和一要绳索,折回索子来量竿,却比竿尺;如果将绳索对半折后再去量竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果绳索对半折后再去量竿,就比竿短5尺.设绳索长
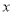 尺,竿长
尺,竿长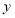 尺,则符合题意的方程组是( )
尺,则符合题意的方程组是( )A.
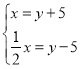 B.
B. 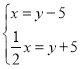 C.
C. 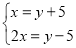 D.
D. 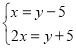
相关试题

