【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
参考答案:
【答案】证明:(1)在平行四边形ABCD中,∠A=∠C,
又∵AE=CG,AH=CF,
∴△AEH≌△CGF.
∴EH=GF.
在平行四边形ABCD中,AB=CD,AD=BC,
∴AB﹣AE=CD﹣CG,AD﹣AH=BC﹣CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,∴△BEF≌△DGH.
∴GH=EF.
∴四边形EFGH是平行四边形.
(2)解法一:在平行四边形ABCD中,AB∥CD,AB=CD.
设∠A=α,则∠D=180°﹣α.
∵AE=AH,∴∠AHE=∠AEH=![]() =90
=90![]() -
-![]() . ∵AD=AB=CD,AH=AE=CG,
. ∵AD=AB=CD,AH=AE=CG,
∴AD﹣AH=CD﹣CG,即DH=DG.
∴∠DHG=∠DGH= ![]() .
.
∴∠EHG=180°﹣∠DHG﹣∠AHE=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.
解法二:连接BD,AC.
∵AH=AE,AD=AB,
∴ ![]() =
=![]() ,∴HE∥BD,
,∴HE∥BD,
同理可证,GH∥AC,
∵四边形ABCD是平行四边形且AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,∴∠EHG=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.
【解析】(1)易证得△AEH≌△CGF,从而证得BE=DG,DH=BF.故有,△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证.
(2)由题意知,平行四边形ABCD是菱形,连接AC,BD,则有AC⊥BD,由AB=AD,且AH=AE可证得HE∥BD,同理可得到HG∥AC,故HG⊥HE,又由1知四边形HGFE是平行四边形,故四边形HGFE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
大家知道
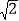 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此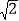 的小数部分我们不可能完全地写出来,于是小明用
的小数部分我们不可能完全地写出来,于是小明用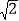 ﹣1来表示
﹣1来表示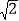 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为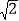 的整数部分是1,用这个数减去其整数部分,差就是小数部分.
的整数部分是1,用这个数减去其整数部分,差就是小数部分.请解答下列问题:
(1)求出
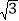 +2的整数部分和小数部分;
+2的整数部分和小数部分;(2)已知:10+
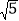 =x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后到达中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.
如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:

(1)图中自变量是 ,因变量是 ;
(2)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(3)小明出发 小时后爸爸驾车出发;
(4)小明从中心书城到滨海公园的平均速度是多少?小明爸爸驾车的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一底角平分线与另一腰所成锐角为75°,则等腰三角形的顶角的大小为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,过直线AC上一点G作y轴的平行线交抛物线一点F,是否存在点F,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
相关试题

