【题目】在矩形ABCD中,AB=6,BC=12,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C,D的对应点分别为C′,D′,折痕与边AD交于点F,当点B,C′,D′恰好在同一直线上时,AF的长为_____.
参考答案:
【答案】8+![]() 或8﹣
或8﹣![]() .
.
【解析】分析: 由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,在Rt△BC′E中,由![]() =2,得到∠C′BE=30°,①当点C′在BC的上方时,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形根据等边三角形的性质和矩形的性质,即可得到AF的长;②当点C′在BC的下方时,过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形根据矩形的性质和等边三角形的性质,即可得到AF的长.
=2,得到∠C′BE=30°,①当点C′在BC的上方时,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形根据等边三角形的性质和矩形的性质,即可得到AF的长;②当点C′在BC的下方时,过F作FG⊥AD于G,D′F交BE于H,同①可得四边形ABGF是矩形根据矩形的性质和等边三角形的性质,即可得到AF的长.
详解: 由折叠的性质得,∠EC′D′=∠C=90°,C′E=CE,
∵点B、C′、D′在同一直线上,
∴∠BC′E=90°,
∵BC=12,BE=2CE,
∴BE=8,C′E=CE=4,
在Rt△BC′E中,![]() =2,
=2,
∴∠C′BE=30°,
①当点C′在BC的上方时,

如图1,过E作EG⊥AD于G,延长EC′交AD于H,则四边形ABEG是矩形,
∴EG=AB=6,AG=BE=8,
∵∠C′BE=30°,∠BC′E=90°,
∴∠BEC′=60°,
由折叠的性质得,∠C′EF=′CEF,
∴∠C′EF=∠CEF=60°,
∵AD∥BC
∴∠HFE=∠CEF=60°,
∴△EFH是等边三角形,
∴在Rt△EFG中,EG=6,
∴GF=2![]() ,
,
∴AF═8+2![]() ;
;
②当点C′在BC的下方时,
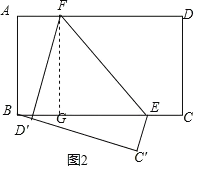
如图2,过F作FG⊥AD于G,D′F交BE于H,
同①可得,四边形ABGF是矩形,△EFH是等边三角形,
∴AF=BG,FG=AB=6,∠FEH=60°,
在Rt△EFG中,GE=2![]() ,
,
∵BE=8,
∴BG=82![]() ,
,
∴AF=82![]() ,
,
综上所述,AF的长是8+2![]() 或82
或82![]() .
.
故答案为:8+2![]() 或82
或82![]() .
.
点睛: 本题考查了翻折变换折叠问题,正确的作出图形是解题的关键.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
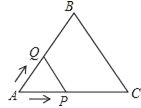
A.
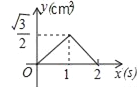 B.
B. 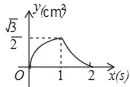
C.
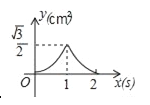 D.
D. 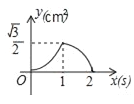
-
科目: 来源: 题型:
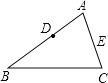
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=8,D是AB的中点.若在AC上存在一点E,使得△ADE与原三角形相似.
(1)确定E的位置,并画出简图:
(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中
中 且
且 ,又
,又 、
、 为
为 的三等分点.
的三等分点.
(1)求证
 ;
;(2)证明:
 ;
;(3)若点
 为线段
为线段 上一动点,连接
上一动点,连接 则使线段
则使线段 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由) -
科目: 来源: 题型:
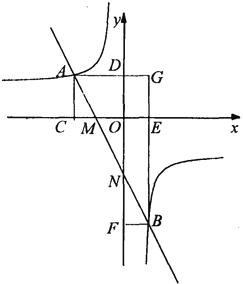
查看答案和解析>>【题目】直线MN与x轴、y轴分别交于点M、N,并且经过第二、三、四象限,与反比例函数y=
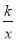 (k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.(1)比较大小:S矩形ACOD S矩形BEOF(填“>,=,<”).
(2)求证:①AGGE=BFBG;
②AM=BN;
(3)若直线AB的解析式为y=﹣2x﹣2,且AB=3MN,则k的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)



按上面方法继续下去,第20个图有_____个三角形;第n个图中有_____个三角形.(用n的代数式表示结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,⊙B的半径为2,点P是⊙B上的一个动点,则PD﹣
 PC的最大值为_____.
PC的最大值为_____.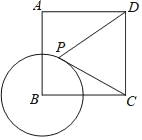
相关试题

