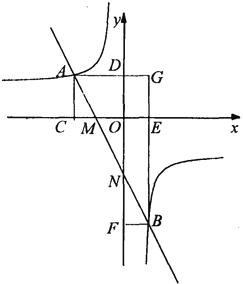
【题目】直线MN与x轴、y轴分别交于点M、N,并且经过第二、三、四象限,与反比例函数y=![]() (k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(1)比较大小:S矩形ACOD S矩形BEOF(填“>,=,<”).
(2)求证:①AGGE=BFBG;
②AM=BN;
(3)若直线AB的解析式为y=﹣2x﹣2,且AB=3MN,则k的值为 .
参考答案:
【答案】(1)=;(2)①见解析,②见解析;(3)﹣4.
【解析】
(1)根据反比例函数的比例系数的几何意义即可作出判断;
(2)①设A的横坐标是a,B的横坐标是b,分别代入y=![]() ,则A的坐标是(a,
,则A的坐标是(a,![]() ),B的坐标是(b,
),B的坐标是(b,![]() ),利用a、b表示出AG、GE、BF、BG的长,即可证得;
),利用a、b表示出AG、GE、BF、BG的长,即可证得;
②求得直线AB的解析式,即可求得M的坐标,即可证明CM=BF,即可证得△ACM≌△NFB,根据全等三角形的对应边相等,即可证得;
(3)根据AM=BN,且AB=3MN,可以得到AM=BN=MN,则OF=2ON,OM=BF,在y=﹣2x﹣2中,求得M、N的坐标,即可求得B的坐标,代入反比例函数解析式即可求得k的值.
(1)根据反比例函数k的几何意义可得:S矩形ACOD=S矩形BEOF=|k|,
故答案为:=;
(2)①设A的横坐标是a,B的横坐标是b,分别代入y=![]() ,则A的坐标是(a,
,则A的坐标是(a,![]() ),B的坐标是(b,
),B的坐标是(b,![]() ),
),
则AG=b﹣a,GE=![]() ,BF=b,BG=
,BF=b,BG=![]() ﹣
﹣![]() ,
,
则AGGE=(b﹣a)![]() =
=![]() ,
,
BFBG=b(![]() ﹣
﹣![]() )=
)=![]() ,
,
∴AGGE=BFBG;
②设过A、B的直线的解析式是y=mx+n,则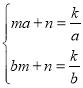 ,
,
解得: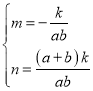 ,
,
则函数的解析式是:y=﹣![]() x+
x+![]() ,
,
令y=0,解得:x=a+b,
则M的横坐标是a+b,
∴CM=a+b﹣a=b,
∴CM=BF,
则△ACM≌△NFB,
∴AM=BN;
(3)∵AM=BN,且AB=3MN,
∴AM=BN=MN,
∴ON=NF,
在y=﹣2x﹣2中,令x=0,解得:y=﹣2,
则ON=2,
令y=0,解得:x=﹣1,则OM=1,
∴OF=2ON=4,OM=BF=1
∴B的坐标是(1,﹣4),
把(1,﹣4)代入y=![]() 中,得:k=﹣4,
中,得:k=﹣4,
故答案为:﹣4.
-
科目: 来源: 题型:
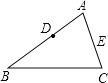
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=8,D是AB的中点.若在AC上存在一点E,使得△ADE与原三角形相似.
(1)确定E的位置,并画出简图:
(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中
中 且
且 ,又
,又 、
、 为
为 的三等分点.
的三等分点.
(1)求证
 ;
;(2)证明:
 ;
;(3)若点
 为线段
为线段 上一动点,连接
上一动点,连接 则使线段
则使线段 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=6,BC=12,点E在边BC上,且BE=2CE,将矩形沿过点E的直线折叠,点C,D的对应点分别为C′,D′,折痕与边AD交于点F,当点B,C′,D′恰好在同一直线上时,AF的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)



按上面方法继续下去,第20个图有_____个三角形;第n个图中有_____个三角形.(用n的代数式表示结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,⊙B的半径为2,点P是⊙B上的一个动点,则PD﹣
 PC的最大值为_____.
PC的最大值为_____.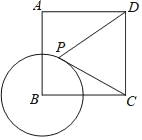
-
科目: 来源: 题型:
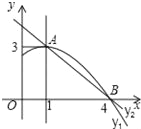
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③b2﹣4ac>0;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1;
⑥方程ax2+bx+c=3有两个相等的实数根.
其中正确的有_____.
相关试题

