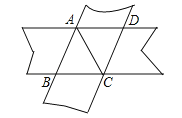
【题目】如图所示,将两条等宽的纸条重叠在一起,得到四边形![]() ,若
,若![]() ,则
,则![]() ___.
___.
参考答案:
【答案】![]()
【解析】分析:首先可证明ABCD是菱形,再由∠ABC=60°和菱形的性质可得△ABC是等边三角形,得AC=AB=8,再由菱形的面积=底×高=对角线乘积÷2即可得到结论.
详解:如图,作BE⊥AD于点E,BF⊥DC于点F,由题意知,纸条等宽,即有:BE=BF,∵AE∥BC,∴∠EAB=∠ABC,∵AB∥FC,∴∠ABC=∠FCB,又∵BE=BF,∠AEB=∠BFC=90°,∴△AEB≌△CFB(ASA),∴AB=BC,∵∠ABC=60°,
∴△ABC是等边三角形,∴AC=AB=8.
∵AD∥BC,∴∠EAB=∠ABC=60°,∴∠EBA=30°,∴AE=4,BE=![]() AE=
AE=![]() .
.
∵S四边形ABCD=AD×BE=![]() AC×BD,∴BD=
AC×BD,∴BD=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3交y轴于点C,直线l为抛物线的对称轴,点P在第三象限且为抛物线的顶点.P到x轴的距离为
 ,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B.
,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B. 
(1)求抛物线的表达式;
(2)直线y= x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y=
x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y=  x+m的表达式;
x+m的表达式;
(3)若N为平面直角坐标系内的点,在直线y= x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元,若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案.
-
科目: 来源: 题型:
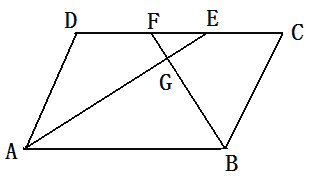
查看答案和解析>>【题目】平行四边形ABCD中, AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.
(1)求证AE⊥BF
(2)判断DE和CF的大小关系,并说明理由.
-
科目: 来源: 题型:
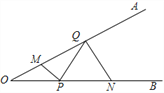
查看答案和解析>>【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD与正五边形EFGHM的边长相等,初始如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合…按这样的方式将正方形依次绕点H、M、E旋转后,正方形中与EF重合的是( )

A.AB
B.BC
C.CD
D.DA
相关试题

