【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次 | 第2次 | 第3次 | |
提现金额(元) | A | b |
|
手续费(元) | 0 | 0.4 | 3.4 |
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.
参考答案:
【答案】(1)0.6;(2)小明第一次提现金额600元,第二次提现800元,第三次提现3400元 (3)![]() 元
元
【解析】
(1)根据应付手续费=(提现金额-1000)×0.1%,即可求出结论;
(2)根据支付的手续费及第三次提现支付的手续费,即可得出关于a,b的二元一次方程组,解之即可求出a,b的值,将其代入3a+2b中即可求出结论;
(3)根据小红共支付手续费2.4元可知第一次和第二次提现超出1000元的部分大于2300元,小于或等于2400元,据此列不等式组即可求出结论.
(1)(1600-1000)×0.1%=0.6(元);
(2)根据题意,得
![]()
解得![]()
∴![]()
答:小明第一次提现金额600元,第二次提现800元,第三次提现3400元 ;
(3)设小红第二次提现金额x元
![]() 元
元
![]()
解得:![]()
答:小红第二次提现金额范围为![]() 元.
元.
故答案为:(1)0.6;(2)小明第一次提现金额600元,第二次提现800元,第三次提现3400元 (3)![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式
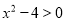 .
.解∵
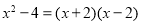 ,∴
,∴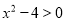 可化为
可化为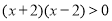 .
.由有理数的乘法法则:两数相乘,同号得正,得:①
 ②
②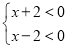
解不等式组①,得
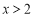 ,解不等式组②,得
,解不等式组②,得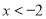
∴
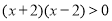 的解集为
的解集为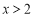 或
或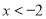 .
.即一元二次不等式
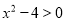 的解集为
的解集为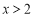 或
或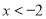 .
.(1)一元二次不等式
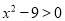 的解集为____________;
的解集为____________;(2)试解一元二次不等式
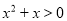 ;
;(3)试解不等式
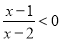 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一条件下,对同一型号的汽车进行耗油1升所行驶路程的实验,将收集到的数据作为一个样本进行分析,绘制出部分频数分布直方图和部分扇形统计图.如下图所示(路程单位:km)


结合统计图完成下列问题:
(1)扇形统计图中,表示12.5≤x<13部分的百分数是 ;
(2)请把频数分布直方图补充完整,这个样本数据的中位数落在第 组;
(3)哪一个图能更好地说明一半以上的汽车行驶的路程在13≤x<14之间?哪一个图能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O, ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,反比例函数y=
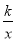 (x>0),过点A(3,4).
(x>0),过点A(3,4).(1)求y关于x的函数表达式.
(2)求当y≥2时,自变量x的取值范围.
(3)在x轴上有一点P(1,0),在反比例函数图象上有一个动点Q,以PQ为一边作一个正方形PQRS,当正方形PQRS有两个顶点在坐标轴上时,画出状态图并求出相应S点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边长为
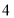 和
和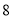 ,则它腰上的高长度为______.
,则它腰上的高长度为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
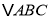 中,已知
中,已知 于点
于点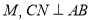 于点
于点 ,
, 为
为 边的中点,连接
边的中点,连接 ,则下列结论:①
,则下列结论:① ;②
;② ;③
;③ 为等边三角形;④当
为等边三角形;④当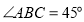 时,
时,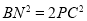 .其中正确的是____________(填写序号).
.其中正确的是____________(填写序号).
相关试题

