【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
参考答案:
【答案】(1)证明见解析;(2)6.
【解析】
试题分析:(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可.
(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
试题解析:(1)连接OD;
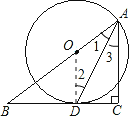
∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC.
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(2)过点D作DE⊥AB,
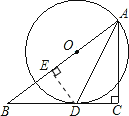
∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得:BE=![]() =4,
=4,
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴![]() .
.
∴![]() .
.
∴AC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,在□ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,
速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,
点Q也停止移动,如图②.设移动时间为t (s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
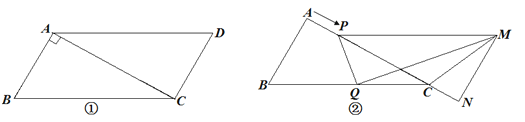
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使
 ?若存在,求出t的值;若不存在,请说明理由;
?若存在,求出t的值;若不存在,请说明理由;(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.

(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若
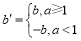 ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
(1)①点(
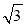 ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;②在点A(-2,-1),B(-1,2)中有一个点是函数y=
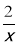 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围;
(3)若点P在关于x的二次函数y= x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式并直接写出s的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,如果斜边上的中线CD=4cm,那么斜边AB= cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
相关试题

