【题目】已知:如图①,在□ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,
速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,
点Q也停止移动,如图②.设移动时间为t (s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
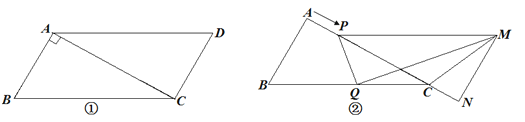
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使![]() ?若存在,求出t的值;若不存在,请说明理由;
?若存在,求出t的值;若不存在,请说明理由;
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】![]()
![]() ;
;![]()
![]() ;
;![]() S△QMC:
S△QMC:![]() ;
;![]()
![]() .
.
【解析】
试题分析:![]() 当PQ∥MN时,可得:
当PQ∥MN时,可得:![]() ,从而得到:
,从而得到:![]() ,解方程求出
,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于点
于点![]() ,则可以得到
,则可以得到![]() ,根据相似三角形的性质可以求出
,根据相似三角形的性质可以求出![]() ,
,![]() ,利用三角形的面积公式求出
,利用三角形的面积公式求出![]() 与
与![]() 的关系式;
的关系式;
![]() 根据S△QMC:
根据S△QMC:![]() 可以得到关于
可以得到关于![]() 的方程,解方程求出
的方程,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则△CPD∽△CBA,利用相似三角形的性质可以得到:
,则△CPD∽△CBA,利用相似三角形的性质可以得到:![]()
![]() ,解方程求出
,解方程求出![]() 的值.
的值.
试题解析:(1)如图所示,
若PQ∥MN,则有![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() .
.
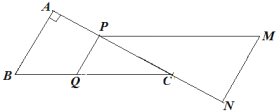
(2)如图所示,
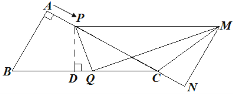
作![]() 于点
于点![]() ,则△CPD∽△CBA,
,则△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
又∵![]() ,
,
∴△QMC的面积为:![]()
(3)存在![]() 时,使得S△QMC:
时,使得S△QMC:![]() .
.
理由如下:
∵PM∥BC
∴![]()
∵S△QMC:![]() ,
,
∴S△PQC: S△ABC=1:5,
∵![]()
.∴![]()
∴![]()
∴![]()
∴存在当![]() 时,S△QMC:
时,S△QMC:![]() ;
;
(4)存在某一时刻![]() ,使
,使![]() .
.
理由如下:
如图所示,
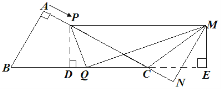
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则△CPD∽△CBA,
,则△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵PQ⊥MQ,
∴△PDQ∽△QEM,
∴![]() ,
,
即![]()
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
即![]() ,
,
∴![]() ,
,![]() (舍去)
(舍去)
∴当![]() 时,使PQ⊥MQ.
时,使PQ⊥MQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式CH4,乙烷的化学式是C2H6,丙烷的化学式是C3H8,…,设碳原子的数目为n(n为正整数),则它们的化学式都可以用下列哪个式子来表示( )
A.CnH2n+2 B.CnH2n C.CnH2n﹣2 D.CnHn+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )
A.8或10
B.8
C.10
D.6或12 -
科目: 来源: 题型:
查看答案和解析>>【题目】与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是( )
A、10x+2y=4 B、4x-y=7 C、20x-4y=3 D、15x-3y=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.

(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若
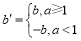 ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5).
(1)①点(
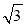 ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;②在点A(-2,-1),B(-1,2)中有一个点是函数y=
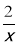 图象上某一个点的限变点,这个点是 ;
图象上某一个点的限变点,这个点是 ;(2)若点P在函数y=-x+3(-2≤x≤k,k>-2)的图象上,其限变点Q的纵坐标b′的取值范围是-5≤b′≤2,求k的取值范围;
(3)若点P在关于x的二次函数y= x2-2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m-n,求s关于t的函数解析式并直接写出s的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
相关试题

