搜索
【题目】Rt△ABC中，如果斜边上的中线CD=4cm，那么斜边AB= cm．
参考答案：
【答案】8
【解析】解：∵Rt△ABC中，斜边上的中线CD=4cm，
∴AB=8cm，
所以答案是：8．
【考点精析】根据题目的已知条件，利用直角三角形斜边上的中线的相关知识可以得到问题的答案，需要掌握直角三角形斜边上的中线等于斜边的一半．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小红将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°时，感觉最舒适（如图1），侧面示意图为图2；使用时为了散热，她在底板下面垫入散热架ACO＇后，电脑转到AO＇B＇位置（如图3），侧面示意图为图4．已知OA=OB=24cm，O＇C⊥OA于点C，O＇C=12cm.
（1）求∠CAO＇的度数．
（2）显示屏的顶部B＇比原来升高了多少？
（3）如图4，垫入散热架后，要使显示屏O＇B＇与水平线的夹角仍保持120°，则显示屏O＇B＇应绕点O＇按顺时针方向旋转多少
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，对于点P(a，b)和点Q(a，b′)，给出如下定义：
若
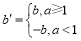，则称点Q为点P的限变点．例如：点(2，3)的限变点的坐标是(2，3)，点(－2，5)的限变点的坐标是(－2，－5)．
（1）①点(
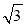，1)的限变点的坐标是 ；②在点A(－2，－1)，B(－1，2)中有一个点是函数y=
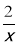图象上某一个点的限变点，这个点是 ；（2）若点P在函数y=－x＋3(－2≤x≤k，k＞－2)的图象上，其限变点Q的纵坐标b′的取值范围是－5≤b′≤2，求k的取值范围；
（3）若点P在关于x的二次函数y= x2－2tx＋t2＋t的图象上，其限变点Q的纵坐标b′的取值范围是b′≥m或b′＜n，其中m＞n．令s=m－n，求s关于t的函数解析式并直接写出s的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°,AD是∠BAC的平分线，O是AB上一点,以OA为半径的⊙O经过点D。
（1）求证：BC是⊙O切线；
（2）若BD=5,DC=3,求AC的长。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.
(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明；
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论，请用简洁的语言表达BD与DE,CE的数量关系。
-
科目： 来源： 题型：
查看答案和解析>>【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2，3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ ABC中，∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°，∠ ACB=50°，则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°，则∠BOC=________
(3)若∠A=70°，则∠BOC=_________
(4)若∠BOC=140°，则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
相关试题
