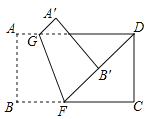
【题目】如图,一张矩形纸片![]() .点
.点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 分别落在点
分别落在点![]() 处,
处,
(1)若![]() ,则
,则![]() 的度数为 °;
的度数为 °;
(2)若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)根据折叠可得∠BFG=∠GFB′,再根据矩形的性质可得∠DFC=40°,从而∠BFG=70°即可得到结论;
(2) 首先求出GD=9-![]() =
=![]() ,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=
,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=![]() ,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
(1)根据折叠可得∠BFG=∠GFB′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DGF=∠BFG,∠ADF=∠DFC,
∵![]()
∴∠DFC=40°
∴∠BFD=140°
∴∠BFG=70°
∴∠DGF=70°;
(2)∵AG=![]() ,AD=9,
,AD=9,
∴GD=9-![]() =
=![]() ,
,
∵四边形ABCD是矩形,
∴AD∥BC,BC=AD=9,
∴∠DGF=∠BFG,
由翻折不变性可知,∠BFG=∠DFG,
∴∠DFG=∠DGF,
∴DF=DG=![]() ,
,
∵CD=AB=4,∠C=90°,
∴在Rt△CDF中,由勾股定理得: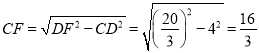 ,
,
∴BF=BC-CF=9-![]() ,
,
由翻折不变性可知,FB=FB′=![]() ,
,
∴B′D=DF-FB′=![]() -
-![]() =3.
=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列解题过程填空:
如图,
 是
是 的平分线,
的平分线, 是
是 的平分线,
的平分线, ,
, ,求
,求 的度数.
的度数.
解:∵
 平分
平分 ,
, 平分
平分 ,
, ,
, ,
,∴
 ①
①  ②
②  ,
,∴
 ③
③  ④
④  ,
,∵
 平分
平分 ,
,∴
 ⑤
⑤  ④
④  ,
,∴
 ⑦
⑦  ⑧
⑧ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中E是BC边上一点,且AB=AE,AE,DC的延长线相交于点F.
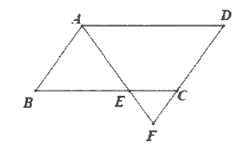
(1)若∠F=62°,求∠D的度数;
(2)若BE=3EC,且△EFC的面积为1,求平行四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l的解析式为y=-
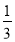 x+
x+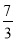 ,与x轴,y轴分别交于A,B两点,双曲线
,与x轴,y轴分别交于A,B两点,双曲线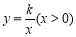 与直线l交于E,F两点,点E的横坐标为1.
与直线l交于E,F两点,点E的横坐标为1.(1)求k的值及F点的坐标;
(2)连接OE,OF,求△EOF的面积;
(3)若点P是EF下方双曲线上的动点(不与E,F重合),过点P作x轴,y轴的垂线,分别交直线l于点M,N,求
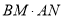 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中,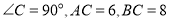 ,点
,点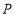 以每秒1个单位的速度从
以每秒1个单位的速度从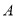 向
向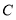 运动,同时点
运动,同时点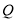 以每秒2个单位的速度从
以每秒2个单位的速度从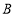 向
向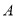 方向运动,
方向运动,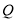 到达
到达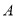 点后,
点后,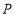 点也停止运动,设点
点也停止运动,设点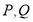 运动的时间为
运动的时间为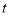 秒.
秒.(1)求
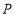 点停止运动时,
点停止运动时,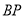 的长;
的长;(2)
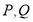 两点在运动过程中,点
两点在运动过程中,点 是
是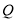 点关于直线
点关于直线 的对称点,是否存在时间
的对称点,是否存在时间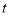 ,使四边形
,使四边形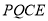 为菱形?若存在,求出此时
为菱形?若存在,求出此时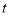 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)
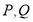 两点在运动过程中,求使
两点在运动过程中,求使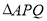 与
与 相似的时间
相似的时间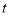 的值.
的值.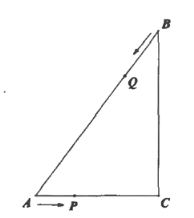
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数
10
15
20
…
x
方式一的总费用(元)
150
175
______
…
______
方式二的总费用(元)
90
135
______
…
______
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
相关试题

