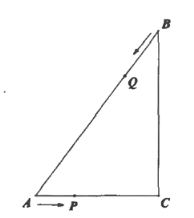
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)求出点Q的从B到A的运动时间,再求出AP的长,利用勾股定理即可解决问题.
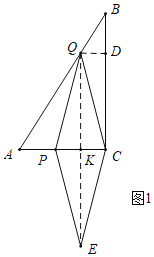
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.根据DQ=CK,构建方程即可解决问题.
(3)分两种情形:如图3-1中,当∠APQ=90°时,如图3-2中,当∠AQP=90°时,分别构建方程即可解决问题.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
点Q运动到点A时,t=![]() =5,
=5,
∴AP=5,PC=1,
在Rt△PBC中,PB=![]() .
.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴![]() ,
,
解得t=![]() .
.
∴t=![]() s时,四边形PQCE是菱形.
s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
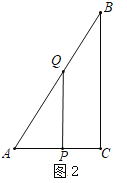
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3中,当∠AQP=90°时,

∵△AQP∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() s时,△APQ是直角三角形.
s时,△APQ是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中E是BC边上一点,且AB=AE,AE,DC的延长线相交于点F.
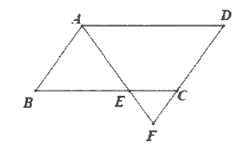
(1)若∠F=62°,求∠D的度数;
(2)若BE=3EC,且△EFC的面积为1,求平行四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张矩形纸片
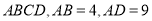 .点
.点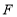 在这张矩形纸片的边
在这张矩形纸片的边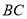 上,将纸片折叠,使
上,将纸片折叠,使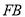 落在射线
落在射线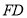 上,折痕为
上,折痕为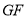 ,点
,点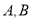 分别落在点
分别落在点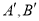 处,
处,(1)若
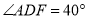 ,则
,则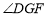 的度数为 °;
的度数为 °;(2)若
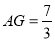 ,求
,求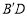 的长.
的长.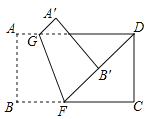
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l的解析式为y=-
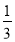 x+
x+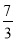 ,与x轴,y轴分别交于A,B两点,双曲线
,与x轴,y轴分别交于A,B两点,双曲线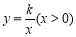 与直线l交于E,F两点,点E的横坐标为1.
与直线l交于E,F两点,点E的横坐标为1.(1)求k的值及F点的坐标;
(2)连接OE,OF,求△EOF的面积;
(3)若点P是EF下方双曲线上的动点(不与E,F重合),过点P作x轴,y轴的垂线,分别交直线l于点M,N,求
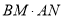 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数
10
15
20
…
x
方式一的总费用(元)
150
175
______
…
______
方式二的总费用(元)
90
135
______
…
______
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用
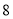 万元购进这种衬衫,面市后果然供不应求.商厦又用
万元购进这种衬衫,面市后果然供不应求.商厦又用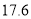 万元购进第二批这种衬衫,所购数量是第一批进量的
万元购进第二批这种衬衫,所购数量是第一批进量的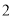 倍,但单价贵了
倍,但单价贵了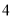 元.商厦销售这种衬衫时每件定价
元.商厦销售这种衬衫时每件定价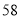 元,最后剩下
元,最后剩下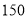 件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元? -
科目: 来源: 题型:
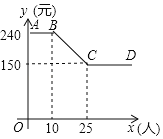
查看答案和解析>>【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
相关试题

