【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
(1)求⊙O的半径的长及线段AD的长;
(2)设PH=x,PC=y,求y关于x的函数关系式.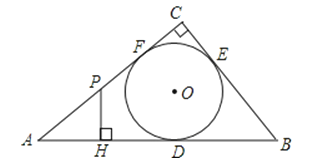
参考答案:
【答案】解:(1)连接AO、DO.设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC=![]() =4,
=4,
则⊙O的半径r=![]() (AC+BC﹣AB)=
(AC+BC﹣AB)=![]() (4+3﹣5)=1;
(4+3﹣5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,CF=CE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC﹣CF=AC﹣OF=4﹣1=3,
即AD=3;
(2)点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴![]() ,
,
即![]()
∴y=﹣![]() x+4,
x+4,
即y与x的函数关系式是y=﹣![]() x+4.
x+4.
【解析】(1)由勾股定理求AC的长度;设⊙O的半径为r,则r=![]() (AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(2)点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知,![]() , 将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式即可.
, 将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式即可.
【考点精析】通过灵活运用三角形的内切圆与内心,掌握三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家居专营店用2730元购进A、B两种新型玻璃保温杯共60个,这两种玻璃保温杯的进价、标价如表所示:
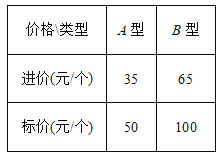
(1)这两种玻璃保温杯各购进多少个?
(2)若A型玻璃保温杯按标价的9折出售,B型玻璃保温杯按标价的8.5折出售,且在运输过程中有2个A型、1个B型玻璃保温杯不慎损坏,不能进行销售,请问这批玻璃保温杯全部售出后,该家居专营店共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,图中点A表示-36,点B表示44,动点P、Q分别从A、B两点同时出发,相向而行,动点P、Q的运动速度比之是3∶2(速度单位:1个单位长度/秒).12秒后,动点P到达原点O,动点Q到达点C,设运动的时间为t(t>0)秒.
(1)求OC的长;
(2)经过t秒钟,P、Q两点之间相距5个单位长度,求t的值;
(3)若动点P到达B点后,以原速度立即返回,当P点运动至原点时,动点Q是否到达A点,若到达,求提前到达了多少时间,若未能到达,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,求d+AB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
相关试题

