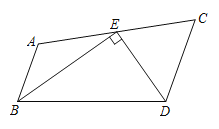
【题目】如图,BE平分∠ABD,DE平分∠CDB相交于AC上一点E,∠BED=90°,求证:AB∥CD.
参考答案:
【答案】证明见解析.
【解析】试题分析:先由三角形内角和定理得出∠EBD+∠EDB=90°,再根据角平分线定义得出∠ABD=2∠EBD,∠CDB=2∠EDB,代入上式即可得出∠ABD+∠CDB=180°,然后根据同旁内角互补,两直线平行证明出AB∥CD.
试题解析:在△BDE中,∵∠BED=90°,∠BED+∠EBD+∠EDB=180°,
∴∠EBD+∠EDB=180°-∠BED=180°-90°=90°.
又∵BE平分∠ABD,DE平分∠CDB,
∴∠ABD=2∠EBD,∠CDB=2∠EDB,
∴∠ABD+∠CDB=2(∠EBD+∠EDB)=2×90°=180°,
∴AB∥CD.
-
科目: 来源: 题型:
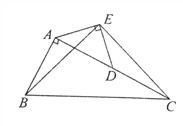
查看答案和解析>>【题目】如图在Rt△ABC中,∠BAC=90 o,AC=2AB,点D是AC的中点,将一块锐角为45 o的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC。试猜想线段BE和EC的数量及位置关系,并证明你的猜想。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x﹣3,用配方法化为y=a(x﹣h)2+k的形式,结果是( )
A.y=﹣(x﹣1)2﹣2
B.y=﹣(x﹣1)2+2
C.y=﹣(x﹣1)2+4
D.y=﹣(x+1)2﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4x+m的顶点在x轴上,则m的值等于( )
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个四边形的边长分别是3,4,5,6,另一个与它相似的四边形最小边长为6,则另一个四边形的最长边是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
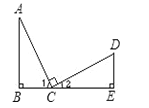
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
相关试题

