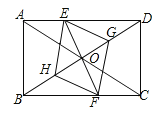
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
参考答案:
【答案】(1)见解析;(2)四边形EGFH是菱形,理由见解析
【解析】
(1)由平行四边形的性质得出AD∥BC,AD=BC,OB=OD,由平行线的性质得出∠FBH=∠EDG,∠OHF=∠OGE,得出∠BHF=∠DGE,求出BF=DE,由AAS即可得出结论;
(2)先证明四边形EGFH是平行四边形,再由等腰三角形的性质得出EF⊥GH,即可得出四边形EGFH是菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
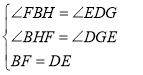 ,
,
∴BFH≌△DEG(AAS);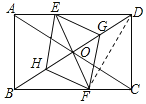
(2)解:四边形EGFH是菱形;理由如下:
连接DF,设EF交BD于O.如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵DE=BF,∠EOD=∠BOF,∠EDO=∠FBO,
∴△EDO≌△FBO,
∴OB=OD,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
-
科目: 来源: 题型:
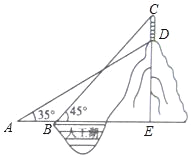
查看答案和解析>>【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈
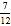 ,cos35°≈
,cos35°≈ ,tan35°≈
,tan35°≈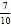 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间
平均数
中位数
众数
甲车间
178
m
183
乙车间
177
182
184
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量
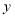 (千克)与每千克售价
(千克)与每千克售价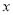 (元)的关系如表所示:
(元)的关系如表所示:每千克售价
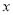 (元)
(元)25
30
40
每周销售量
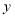 (千克)
(千克)240
200
150
(1)求出每周销售量
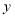 (千克)与每千克售价
(千克)与每千克售价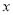 (元)的函数关系式.
(元)的函数关系式.(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否达到每周获利2000元?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜坡AB长10米,按图中的直角坐标系可用
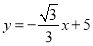 表示,点A,B分别在x轴和y轴上,且
表示,点A,B分别在x轴和y轴上,且 .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用
.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用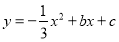 表示.
表示.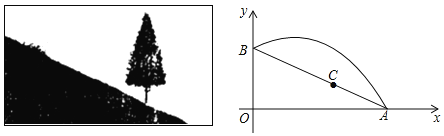
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
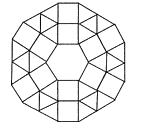
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
-
科目: 来源: 题型:
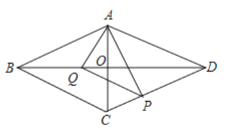
查看答案和解析>>【题目】菱形
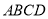 中,对角线
中,对角线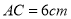 ,
,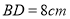 ,动点
,动点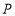 、
、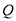 分别从点
分别从点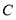 、
、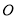 同时出发,运动速度都是
同时出发,运动速度都是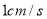 ,点
,点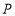 由
由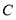 向
向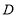 运动;点
运动;点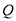 由
由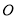 向
向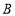 运动,当
运动,当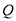 到达点
到达点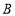 时,
时,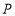 ,
,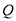 两点运动停止,设时间为
两点运动停止,设时间为 秒
秒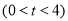 .连接
.连接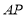 ,
,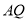 ,
, .
.
(1)当
 为何值时,
为何值时,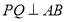 ;
;(2)设
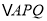 的面积为
的面积为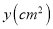 ,请写出
,请写出 与
与 的函数关系式;
的函数关系式;(3)当
 为何值时,
为何值时,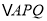 的面积是四边形
的面积是四边形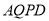 面积的
面积的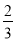 ;
;(4)是否存在
 值,使得线段
值,使得线段 经过
经过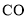 的中点
的中点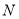 ;若存在,求出
;若存在,求出 值;若不存在,请说明理由.
值;若不存在,请说明理由.
相关试题

