【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间 | 平均数 | 中位数 | 众数 |
甲车间 | 178 | m | 183 |
乙车间 | 177 | 182 | 184 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.
参考答案:
【答案】(1)177.5;(2)甲;甲车间生产的产品合格率为70%,乙车间生产的产品合格率<50%;(3)280.
【解析】
(1)根据扇形图给出的各组产品的百分比、中位数的概念计算;
(2)求出甲、乙两车间生产的产品合格率,比较得到答案;
(3)根据甲车间生产的产品合格率为70%计算.
(1)由扇形统计图可知,A组数据的个数:5%×20=1,
B组数据的个数:20%×20=4,
C组数据的个数:45%×20=9,
∴m=![]() ×(177+178)=177.5,
×(177+178)=177.5,
故答案为177.5;
(2)甲、乙两车间生产的产品合格率更高的是甲,
理由如下:甲车间生产的产品合格率为:![]() ×100%=70%,
×100%=70%,
∵乙车间生产的产品的中位数是182,
∴乙车间生产的产品合格率<50%,
故答案为甲;甲车间生产的产品合格率为70%,乙车间生产的产品合格率<50%;
(3)∵甲车间生产的产品合格率为70%,
∴估计甲车间生产该款新产品中合格产品有:400×70%=280,
故答案为280.
-
科目: 来源: 题型:
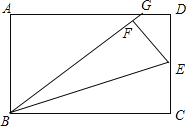
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若
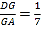 ,则
,则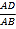 =__.
=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
-
科目: 来源: 题型:
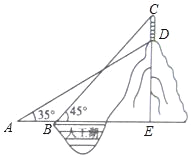
查看答案和解析>>【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈
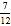 ,cos35°≈
,cos35°≈ ,tan35°≈
,tan35°≈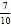 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量
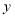 (千克)与每千克售价
(千克)与每千克售价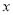 (元)的关系如表所示:
(元)的关系如表所示:每千克售价
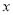 (元)
(元)25
30
40
每周销售量
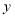 (千克)
(千克)240
200
150
(1)求出每周销售量
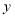 (千克)与每千克售价
(千克)与每千克售价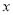 (元)的函数关系式.
(元)的函数关系式.(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否达到每周获利2000元?说明理由.
-
科目: 来源: 题型:
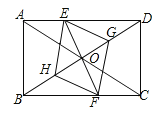
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜坡AB长10米,按图中的直角坐标系可用
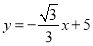 表示,点A,B分别在x轴和y轴上,且
表示,点A,B分别在x轴和y轴上,且 .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用
.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用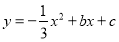 表示.
表示.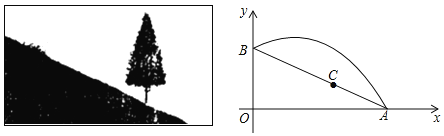
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
相关试题

