【题目】我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
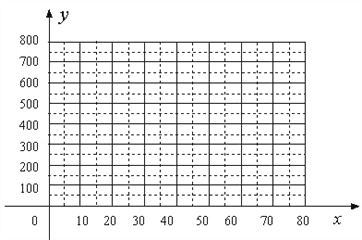
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
参考答案:
【答案】(1)![]() 与
与![]() 的函数关系是一次函数的关系,
的函数关系是一次函数的关系,
函数关系式为y=-10x+800 (20<x<80)
(2)设工艺厂试销该工艺品每天获得的利润为L元
则 L=(x-20)(-10x+800)
=-10(x-50)2+9000
∴当销售单价定为50元时,每天获得的利润最大,最大利润是9000元。
(3)由(2)知当x<50时,y随x的增大而增大,
∴当x=45时有最大值,
∴当销售单价定为45元时,每天获得的利润最大
【解析】分析:(1)从表格中的数据我们可以看出当x增加10时,对应y的值减小100,所以y与x之间可能是一次函数的关系,我们可以根据图象发现这些点在一条直线上,所以y与x之间是一次函数的关系,然后设出一次函数关系式,求出其关系式.
(2)利用二次函数的知识求最大值.
解:(1)画图如图;
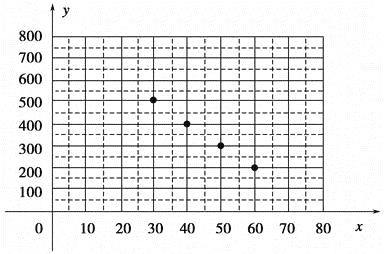
由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0)
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴![]() ,解得
,解得![]()
∴函数关系式是:y=-10x+800.
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=(x-20)(-10x+800)
=-10x2+1000x-16000
=-10(x-50)2+9000
∴当x=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元.
(3)对于函数W=-10(x-50)2+9000,
当x≤45时,W的值随着x值的增大而增大,销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措.二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(生男生女机会均等,且与顺序有关).
(1)该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好是1男1女的概率;
(2)该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中至少有1个女孩的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面每一组数据中的三个数值分别为三角形的三边长,其中错误的是( )
A.4,4,8B.8,8,2C.7,7,7D.3,4,5
-
科目: 来源: 题型:
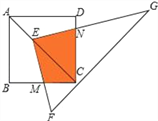
查看答案和解析>>【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A.
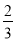 a2 B.
a2 B. 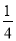 a2 C.
a2 C. 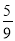 a2 D.
a2 D.  a2
a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣8,0),点P的坐标为(-
 ,0),直线y=
,0),直线y= x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的内角∠ABC与外角∠ACD的平分线交于点E,且CE∥AB,AC与BE交于点E,则下列结论错误的是( )

A.CB=CE
B.∠A=∠ECD
C.∠A=2∠E
D.AB=BF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2
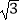 cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 .
cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 . 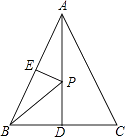
相关试题

