【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )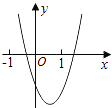
A.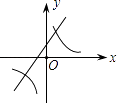
B.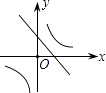
C.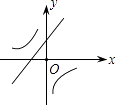
D.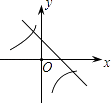
参考答案:
【答案】D
【解析】解:由抛物线的图象可知,横坐标为1的点,即(1,a+b+c)在第四象限,因此a+b+c<0;
∴双曲线 ![]() 的图象在第二、四象限;
的图象在第二、四象限;
由于抛物线开口向上,所以a>0;
对称轴x= ![]() >0,所以b<0;
>0,所以b<0;
抛物线与x轴有两个交点,故b2﹣4ac>0;
∴直线y=bx+b2﹣4ac经过第一、二、四象限.
所以答案是:D.
【考点精析】根据题目的已知条件,利用一次函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
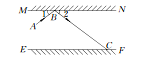
(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E分别是AB,AC的中点,BE是∠ABC的平分线,对于下列结论:①BC=2DE;②DE∥BC;③BD=DE;④BE⊥AC.其中正确的是 ( )
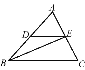
A. ①② B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 的坐标分别是
的坐标分别是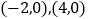 ,现同时将点
,现同时将点 分别向上平移2个单位长度,再向右平移2个单位长度,得到
分别向上平移2个单位长度,再向右平移2个单位长度,得到 的对应点
的对应点 .连接
.连接 .
.(1)写出点
 的坐标并求出四边形
的坐标并求出四边形 的面积.
的面积.(2)在
 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 的面积是
的面积是 面积的2倍?若存在,请求出点
面积的2倍?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)若点
 是直线
是直线 上一个动点,连接
上一个动点,连接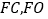 ,当点
,当点 在直线
在直线 上运动时,请直接写出
上运动时,请直接写出 与
与 的数量关系.
的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=4m,∠A=30°,则DE等于( )
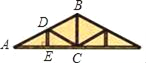
A. 1m B. 2m C. 3m D. 4m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
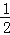 BC,连接CD和EF.
BC,连接CD和EF.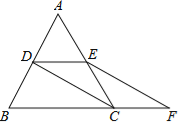
(1)求证:DE=CF;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是 .
相关试题

