【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.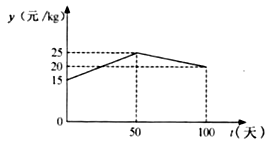
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
参考答案:
【答案】
(1)
解:依题可得: ![]()
解得 ![]()
答:a的值为0.04,b的值为30.
(2)
解:①当0≤t≤50时,设y与t的函数关系式为y=k1t+n1.
把点(0,15),(50,25)的坐标分别代入得:![]()
解得: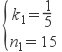
∴y与t的函数关系式为y=![]() t+15.
t+15.
当50<t≤100时,设y与t的函数关系式为y=k2t+n2.
把点(50,25)和(100,20)的坐标分别代入得 :![]()
解得 :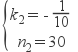
∴y与t的函数关系式为y=-![]() t+30.
t+30.
②由题意得,当0≤t≤50时,
W=20000×(![]() t+15)-(400t+300000)=3600t
t+15)-(400t+300000)=3600t
∵3600>0,∴当t=50时,W最大值=180000(元)
当50<t≤100时,W=(100t+15000)(-![]() t+30)-(400t+300000)=-10t2+1100t+150000=-10(t-55)2+180250
t+30)-(400t+300000)=-10t2+1100t+150000=-10(t-55)2+180250
∵-10<0,∴当t=55时,W最大值=180250
综上所述,当t为55天时,W最大,最大值为180250元.
【解析】(1)根据题意,列方程组求解即可.
(2)通过图像找到相应的点的坐标,根据待定系数法分类列出方程组即可得到函数解析式;然后根据利润=销售总额-总成本=销售单价×销售天数-(放养总费用+收购成本),然后根据一次函数的特点和二次函数的最值求解即可.
【考点精析】本题主要考查了解二元一次方程组和确定一次函数的表达式的相关知识点,需要掌握二元一次方程组:①代入消元法;②加减消元法;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,推理填空:

(1)∵∠1=_______(已知),
∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=______(已知),
∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+_______=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2019分钟时,这个粒子所在位置的坐标是( )
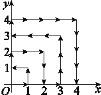
A. (44,5) B. (5,44) C. (44,6) D. (6,44)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中, 放置一副三角板 ABO(OAB 90 ,OBA AOB 45 ,OA AB) , BO 边与 x 轴重合,其中一个45角的顶点在原点O ,直角顶点 A 在第一象限内.
(1)将另一个三角板 DEF 如图 1 放置, EDF 90 ,直角顶点 D 置于 AO 边上(不与O 重合),此时, DE 交 y 轴于 M 点, DF 交 x 轴于 N 点,求证:DM DN .
(2)如图 2, D 是线段 AB 上一动点,连接OD ,过O 作OE OD ,取点 E 满足OE OD .连接 EB 交OA 于点 P ,探究
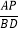 的值是否为定值,若是定值,求出其值;若不是定值,说明理由.
的值是否为定值,若是定值,求出其值;若不是定值,说明理由.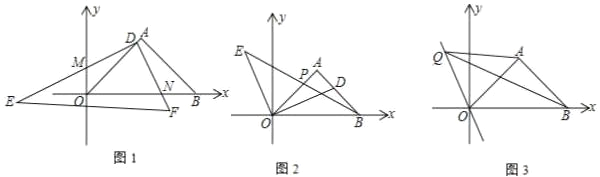
(3)如图 3,直线a 经过原点且与 y 轴成22.5角,Q 是 x 轴上方直线a 上一动点,连接 AQ 、 BQ ,请比较OB OA 与QA QB 的大小关系,并说明理由.
相关试题

