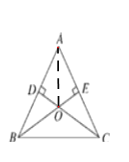
【题目】如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,∠A=60°.
(1)求证:△ABC是等边三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.

参考答案:
【答案】(1)见解析;(2) 点O在∠BAC的平分线上,理由见解析.
【解析】
(1)由OB=OC,得∠OBC=∠OCB.再证∠BEC=∠CDB=90°由(AAS)可证△BCE≌△CBD,则∠DBC=∠ECB,所以,含有60°的等腰三角形是等边三角形;(2)由(1△BCE≌△CBD,得,EB=CD.又OB=OC,所以OE=OD,再由角平分线性质定理可证得.
(1)证明:∵OB=OC,∴∠OBC=∠OCB.
∵BE⊥AC,CD⊥AB,∴∠BEC=∠CDB=90°.
又∵BC=BC,∴△BCE≌△CBD(AAS),
∴∠DBC=∠ECB,∴AB=AC.
又∵∠A=60°,
∴△ABC是等边三角形.
(2)解:点O在∠BAC的平分线上.
理由如下:连接AO.由(1)可知△BCE≌△CBD,∴EB=CD.
∵OB=OC,∴OE=OD.
又∵OE⊥AC,OD⊥AB,
∴点O在∠BAC的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简计算
(1)计算: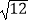 ﹣(
﹣( 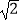 ﹣1)0﹣2cos30°
﹣1)0﹣2cos30°
(2)解方程: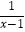 +
+ 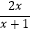 =2.
=2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F.点E是AB的中点,连接EF.

(1)求证:EF∥BC;
(2)若△ABD的面积是6,求四边形BDFE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过点D分别向AB、AC引垂线,垂足分别为点E、F.
(1)如图①,当点D在BC的什么位置时,DE=DF?并证明;
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?请写出所有的全等三角形(不必证明);
(3)如图②,过点C作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学团委会为了解该校学生的课余活动情况,采取抽样的办法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制了如下的两幅不完整的统计图(如图),请你根据图中提供的信息解答下列问题:

(1)这次抽样中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)若该校有2500名学生,你估计全校可能有多少名学生爱好阅读? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
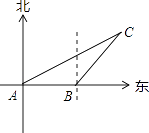
(1)说明点B是否在暗礁区域内;
(2)若继续向东航行有无触礁的危险?请说明理由.
相关试题

