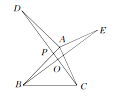
【题目】如图所示,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,AB和CD相交于P,则∠DOE的度数是____.
参考答案:
【答案】90°
【解析】
根据已知条件易证得△AEB≌△ACD,可得∠D=∠ABE,由DA⊥AB可得∠D+∠APD=90°,而由图可知∠APD和∠BPO是对顶角相等,即可得∠DOE=∠DOB=90°.
解:∵DA⊥AB,EA⊥AC,
∴∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
又∵AB=AD,AC=AE,
∴△AEB≌△ACD(SAS),
∴∠D=∠ABE;
∵DA⊥AB,
∴∠D+∠APD=90°,
∵∠APD=∠BPO(对顶角相等),已证得∠D=∠ABE;
∴∠BPO+∠ABE=90°,
∴∠DOE=∠DOB=90°.
故答案为:90°.
-
科目: 来源: 题型:
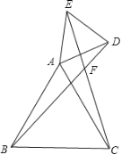
查看答案和解析>>【题目】如图,已知△ABC和△ADE均为等边三角形,BD、CE交于点F.
(1)求证:BD=CE;(2)求锐角∠BFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级的篮球队有10名队员
 在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:进球数
42
32
26
20
19
18
人数
1
1
2
1
2
3
针对这次训练,请解答下列问题:
 求这10名队员进球数的平均数、中位数;
求这10名队员进球数的平均数、中位数; 求这支球队投篮命中率______;
求这支球队投篮命中率______;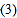 若队员小亮“二分球”的投篮命中率为
若队员小亮“二分球”的投篮命中率为 ,请你分析一下小亮在这支球队中的投篮水平.
,请你分析一下小亮在这支球队中的投篮水平. 投篮命中率
投篮命中率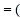 进球数
进球数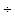 投篮次数
投篮次数
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: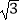 (
( 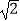 +
+ 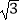 )﹣
)﹣ 
(2)解方程:x2﹣2x=4. -
科目: 来源: 题型:
查看答案和解析>>【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
相关试题

