【题目】在△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC= 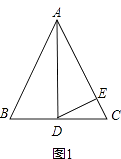
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= 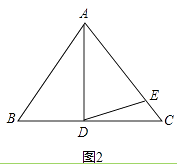
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由. 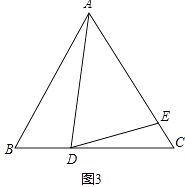
参考答案:
【答案】
(1)15°
(2)20°
(3)∠EDC= ![]() ∠BA
∠BA
(4)解:仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC
【解析】解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°.(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°.(3)∠BAD=2∠EDC(或∠EDC= ![]() ∠BAD)
∠BAD)
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式2x2﹣3x+5是次项式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+3x+5的值为9,则代数式3x2+9x﹣2的值为( )
A. 4 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.﹣4的算术平方根是2
B.﹣ 是2的一个平方根
是2的一个平方根
C.(﹣1)2的立方根是﹣1
D. =±5
=±5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD=AE,AD与BE相交于点F.
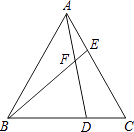
(1)求证:AD=BE;
(2)求∠BFD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.
B.
C.
D.
相关试题

