【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:根据题意画出相应的图形,如图所示:
在Rt△ABC中,AC=9,BC=12,
根据勾股定理得:AB= ![]() =15,
=15,
过C作CD⊥AB,交AB于点D,
又S△ABC= ![]() ACBC=
ACBC= ![]() ABCD,
ABCD,
∴CD= ![]() =
= ![]() =
= ![]() ,
,
则点C到AB的距离是 ![]() .
.
故选A
根据题意画出相应的图形,如图所示,在直角三角形ABC中,由AC及BC的长,利用勾股定理求出AB的长,然后过C作CD垂直于AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,将AC,AB及BC的长代入求出CD的长,即为C到AB的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=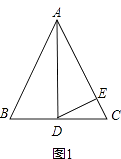
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=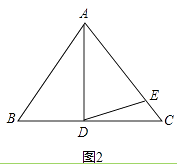
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.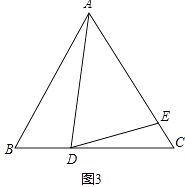
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.﹣4的算术平方根是2
B.﹣ 是2的一个平方根
是2的一个平方根
C.(﹣1)2的立方根是﹣1
D. =±5
=±5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD=AE,AD与BE相交于点F.
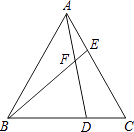
(1)求证:AD=BE;
(2)求∠BFD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在植树节活动中,A班有30人,B班有16人,现要从A班调一部分人去支援B班,使B班人数为A班人数的2倍,那么应从A班调出多少人?如设从A班调x人去B班,根据题意可列方程:__________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】连云港某一天的最高气温是7℃,最低气温是﹣15℃,则这一天的温差是( )
A. 8℃ B. 22℃ C. ﹣8℃ D. ﹣22℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A. 3x+3y=6xy B. x+x=x2
C. 6yx2﹣8x2y=﹣2x2y D. ﹣9y2+6y2=﹣3
相关试题

