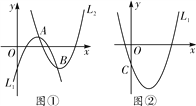
【题目】如图①,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2称为“伴随抛物线”,可见一条抛物线的“伴随抛物线”可以有多条.
(1)抛物线L1:y=-x2+4x-3与抛物线L2是“伴随抛物线”,且抛物线L2的顶点B的横坐标为4,求抛物线L2的表达式;
(2)若抛物线y=a1(x-m)2+n的任意一条“伴随抛物线”的表达式为y=a2(x-h)2+k,请写出a1与a2的关系式,并说明理由;
(3)在图②中,已知抛物线L1:y=mx2-2mx-3m(m>0)与y轴相交于点C,它的一条“伴随抛物线”为L2,抛物线L2与y轴相交于点D,若CD=4m,求抛物线L2的对称轴.
参考答案:
【答案】(1)y=(x-4)2-3(2)伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2(3)抛物线L2的对称轴为x=±2.
【解析】试题分析:(1)先分别求得点A、点B的坐标,然后再利用待定系数法进行求解即可;
(2)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得:(a1+a2 )(m-h)2=0,可得a1=-a2;
(3)易得抛物线L1的顶点坐标为(1,-4m),设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,则有抛物线L2的表达式为y=-mx2+2mhx-2mh-3m,从而得点D的坐标为(0,-2mh-3m),再根据点C的坐标为(0,-3m),从而可得|(-2mh-3m)-(-3m)|=4m,解得h=±2,从而得抛物线L2的对称轴为x=±2.
试题解析:(1)由y=-x2+4x-3可得A的坐标为(2,1),
将x=4代入y=-x2+4x-3,得y=-3,∴B的坐标为(4,-3),
设抛物线L2的解析式为y=a(x-4)2-3; 将(2,1)代入y=a(x-4)2-3,
得1=a(2-4)2-3,解得a=1,
∴抛物线L2的表达式为y=(x-4)2-3;
(2)a1=-a2,理由如下:
∵抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B在抛物线L1上,
∴可列方程组: 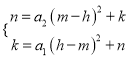 ,
,
整理,得(a1+a2)(m-h)2=0,
∵伴随抛物线的顶点不重合,∴m≠h,∴a1=-a2;
(3)抛物线L1:y=mx2-2mx-3m的顶点坐标为(1,-4m),
设抛物线L2的顶点的横坐标为h,则其纵坐标为mh2-2mh-3m,
∴抛物线L2的表达式为y=-m(x-h)2+mh2-2mh-3m,
化简得,y=-mx2+2mhx-2mh-3m,
所以点D的坐标为(0,-2mh-3m),
又点C的坐标为(0,-3m),
可得|(-2mh-3m)-(-3m)|=4m, 解得h=±2,
∴抛物线L2的对称轴为x=±2.
-
科目: 来源: 题型:
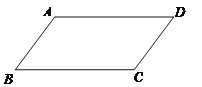
查看答案和解析>>【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
(1)求横档AD的长;
(2)点C离地面的高度.(sin15°=0.26,cos15°=0.97,精确到1cm)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB=90°,∠COD=20°,OM平分∠AOC,ON平分∠BOD.
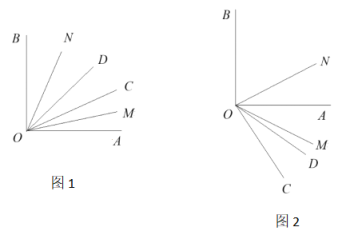
(1)如图1,∠COD在∠AOB内部,且∠AOC=30°.则∠MON的大小为 .
(2)如图1,∠COD在∠AOB内部,若∠AOC的度数未知,是否能求出∠MON的大小,若能,写出你的解答过程;若不能,说明理由.
(3)如图2,∠COD在∠AOB外部(OM在OD上方,∠BOC
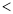 180°),试求出∠MON的大小.
180°),试求出∠MON的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】当你把纸对折一次时,可以得到2层,对折2次时可以得到4层,对折3次时可以得到8层,照这样折下去:
(1)你能发现层数与折纸次数的关系吗?
(2)计算对折5次时的层数;
(3)如果每层纸的厚度是0.05毫米,求对折10次之后纸的总厚度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且
 (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有________名学生参加;
(2)直接写出表中:a= ,b= 。
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
相关试题

