【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)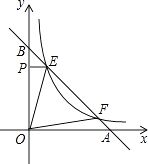
参考答案:
【答案】2;![]()
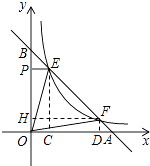
【解析】解:作EC⊥x轴于C,FD⊥x轴于D,FH⊥y轴于H,如图,
∵△OEP的面积为1,
∴ ![]() |k|=1,
|k|=1,
而k>0,
∴k=2,
∴反比例函数解析式为y= ![]() ,
,
∵EP⊥y轴,FH⊥y轴,
∴EP∥FH,
∴△BPE∽△BHF,
∴ ![]() =
= ![]() ,即HF=mPE,
,即HF=mPE,
设E点坐标为(t, ![]() ),则F点的坐标为(tm,
),则F点的坐标为(tm, ![]() ),
),
∵S△OEF+S△OFD=S△OEC+S梯形ECDF ,
而S△OFD=S△OEC=1,
∴S△OEF=S梯形ECDF= ![]() (
( ![]() +
+ ![]() )(tm﹣t)
)(tm﹣t)
=( ![]() +1)(m﹣1)
+1)(m﹣1)
= ![]() .
.
所以答案是:2, ![]() .
.
【考点精析】掌握反比例函数的性质是解答本题的根本,需要知道性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x2)3x的结果是( )
A.﹣6x6
B.8x6
C.﹣8x7
D.8x7 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x﹣1)(x+2)=0的解是( ).
A.x=1B.x=﹣2C.x1=﹣1,x2=2D.x1=1,x2=﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣6x+11的顶点为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交
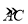 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.(1)求证:DC=DP;
(2)若∠CAB=30°,当F是
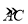 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.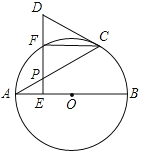
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读运用:
当方程中的系数用字母表示时,这样的方程叫做含字母系数的方程,也叫含参数的方程.
例如:2x+m=4,那么如何解这样的方程呢?实际上,我们可以把m当作常数,解出方程,
解得:2x=4﹣m.
x=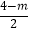 ,
,
请仿照上面的解法解答下列问题:
(1)解关于x,y的二元一次方程组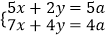 ,
,
(2)若关于x,y的二元一次方程组: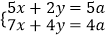 的解满足不等式组
的解满足不等式组 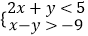 ,求出整数a的所有值.
,求出整数a的所有值. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:xy2﹣9x= .
相关试题

