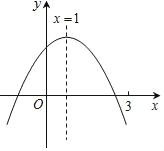
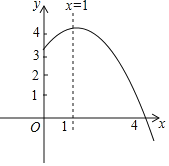
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②3a+c<0;③a+b≥am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.
其中正确的有( )个.
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】B
【解析】
由抛物线开口方向得到a<0,利用抛物线的对称轴方程得到b=-2a>0,由抛物线与x轴的交点位置得到c>0,则可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)与(0,0)之间,所以当x=-1时,a-b+c<0,则可对④进行判断;把b=-2a代入可对②进行判断;利用二次函数的最值问题对③进行判断;把ax12+bx1=ax22+bx2进行变形得到(x1-x2)[a(x1+x2)+b]=0,从而得到a(x1+x2)+b=0,再利用b=-2a可对⑤进行判断.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-![]() =1,
=1,
∴b=-2a>0,
∵抛物线与x轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线与x轴的一个交点在(2,0)与(3,0)之间,
∴抛物线与x轴的另一个交点在(-1,0)与(0,0)之间,
∴当x=-1时,y<0,
即a-b+c<0,所以④错误;
∴a+2a+c<0,即3a+c<0,所以②正确;
∵x=1时,y有最大值,
∴a+b+c≥am2+bm+c,
即a+b≥am2+bm,所以③正确;
∵ax12+bx1=ax22+bx2,
∴a(x1+x2)(x1-x2)+b(x1-x2)=0,
∴(x1-x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,
∴x1+x2=-![]() =-
=-![]() =2,所以⑤正确.
=2,所以⑤正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】建立适当的坐标系,运用函数知识解决下面的问题:
如图,是某条河上的一座抛物线形拱桥,拱桥顶部点E到桥下水面的距离EF为3米时,水面宽AB为6米,一场大雨过后,河水上涨,水面宽度变为CD,且CD=2
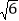 米,此时水位上升了多少米?
米,此时水位上升了多少米?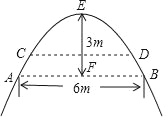
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣bx+2(﹣2≤b≤2),当b从﹣2逐渐增加到2的过程中,它所对应的抛物线的位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( )
A. 先往左上方移动,再往左下方移动
B. 先往左下方移动,再往左上方移动
C. 先往右上方移动,再往右下方移动
D. 先往右下方移动,再往右上方移动
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点M在△ABC内,AM平分∠BAC.点D与点M在AC所在直线的两侧,AD⊥AB,AD=BC,点E在AC边上,CE=AM,连接MD、BE.
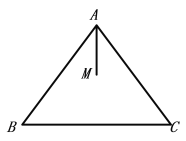
(1)补全图形;
(2)请判断MD与BE的数量关系,并进行证明;
(3)点M在何处时,BM+BE会有最小值,画出图形确定点M的位置;如果AB=5,BC=6,求出BM+BE的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④方程ax2+bc+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣
 ,y1),C(﹣
,y1),C(﹣ ,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )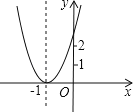
A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】信息1:我们已经学完了解分式方程,它的一般步骤为:确定最简公分母、化为整式方程、求出整式方程的解、进行检验(第一,代入最简公分母验证是否为零,第二代入分式方程的左右两边检验是否相等)、确定分式方程的解.其中代入最简公分母验证这一步也就是在验证所有分式在取此值时是否有意义;
信息2:遇到
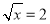 这种特征的题目,可以两边同时平方得到
这种特征的题目,可以两边同时平方得到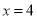 ;
;信息3:遇到
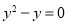 这种特征的题目,可以将左边变形,得到
这种特征的题目,可以将左边变形,得到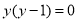 ,进而可以得到
,进而可以得到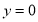 或
或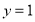 .
.结合上述信息解决下面的问题:
问题1:如果
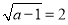 .可得:
.可得: ;
;问题2:解关于b的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
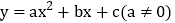 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为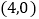 ,抛物线的对称轴是
,抛物线的对称轴是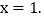 下列结论中:
下列结论中: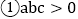 ;
;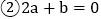 ;
; 方程
方程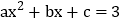 有两个不相等的实数根;
有两个不相等的实数根;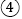 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为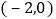 ;
; 若点
若点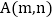 在该抛物线上,则
在该抛物线上,则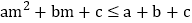 .
.其中正确的有
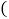
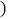
A. 5个 B. 4个 C. 3个 D. 2个
相关试题

