搜索
【题目】建立适当的坐标系，运用函数知识解决下面的问题：
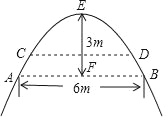
如图，是某条河上的一座抛物线形拱桥，拱桥顶部点E到桥下水面的距离EF为3米时，水面宽AB为6米，一场大雨过后，河水上涨，水面宽度变为CD，且CD=2
米，此时水位上升了多少米？
参考答案：
【答案】上升了1米．
【解析】
以点E为原点、EF所在直线为y轴，垂直EF的直线为x轴建立平面直角坐标系，
设抛物线的解析式为y=kx2（k＜0），根据B点坐标可求出k的值，即可求出二次函数的解析式，把D点坐标代入可求出河水上涨后点E到桥下水面的距离，进而可得答案.
以点E为原点、EF所在直线为y轴，垂直EF的直线为x轴建立平面直角坐标系，
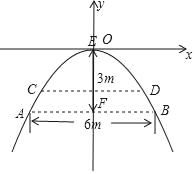
根据题意知E（0，0）、A（﹣3，﹣3）、B（3，﹣3），
设y=kx2（k＜0），
将点（3，﹣3）代入，得：k=﹣
，
∴y=﹣x2，
将x=
代入，得：y=﹣2，
∴上升了1米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某店只销售某种进价为40元/kg的产品，已知该店按60元kg出售时，每天可售出100kg，后来经过市场调查发现，单价每降低1元，则每天的销售量可增加10kg．
（1）若单价降低2元，则每天的销售量是_____千克，每天的利润为_____元；若单价降低x元，则每天的销售量是_____千克，每天的利润为______元；（用含x的代数式表示）
（2）若该店销售这种产品计划每天获利2240元，单价应降价多少元？
（3）当单价降低多少元时，该店每天的利润最大，最大利润是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.
已知：如图，钝角∠AOB.求作：∠AOB的角平分线.
作法：
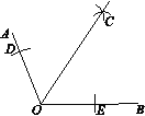
①在OA和OB上，分别截取OD、OE，使OD＝OE；
②分别以D、E为圆心，大于
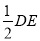的长为半径作弧,在∠AOB内，两弧交于点C；③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
在该作图中蕴含着几何的证明过程：
由①可得：OD＝OE
由②可得：_________________
由③可知：OC＝OC
∴______≌_________（依据：________________________）
∴可得∠COD=∠COE（全等三角形对应角相等）
即OC就是所求作的∠AOB的角平分线.
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们规定在网格内的某点进行一定条件操作到达目标点：H代表所有的水平移动，H1代表向右水平移动1个单位长度，H-1代表向左平移1个单位长度；S代表上下移动，S1代表向上移动1个单位长度，S-1代表向下移动1个单位长度，
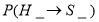表示点P在网格内先一次性水平移动，在此基础上再一次性上下移动；
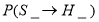表示点P在网格内先一次性上下移动，在此基础上再一次性水平移动.（1）如图，在网格中标出
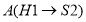移动后所到达的目标点
；
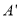（2）如图，在网格中的点B到达目标点A，写出点B的移动方法________________；
（3）如图，在网格内有格点线段AC，现需要由点A出发，到达目标点D,使得A、C、D三点构成的格点三角形是等腰直角三角形，在图中标出所有符合条件的点D的位置并写出点A的移动方法.
-
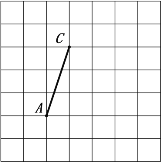
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2﹣bx+2（﹣2≤b≤2），当b从﹣2逐渐增加到2的过程中，它所对应的抛物线的位置也随之变动，下列关于抛物线的移动方向的描述中，正确的是（ ）
A. 先往左上方移动，再往左下方移动
B. 先往左下方移动，再往左上方移动
C. 先往右上方移动，再往右下方移动
D. 先往右下方移动，再往右上方移动
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，点M在△ABC内，AM平分∠BAC.点D与点M在AC所在直线的两侧，AD⊥AB，AD=BC，点E在AC边上，CE=AM，连接MD、BE.
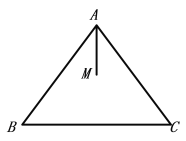
（1）补全图形；
（2）请判断MD与BE的数量关系，并进行证明；
（3）点M在何处时，BM+BE会有最小值，画出图形确定点M的位置；如果AB=5，BC=6，求出BM+BE的最小值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）图象如图，下列结论：
①abc＞0；②3a+c＜0；③a+b≥am2+bm；④a﹣b+c＞0；⑤若ax12+bx1=ax22+bx2，且x1≠x2，则x1+x2=2．
其中正确的有（ ）个．
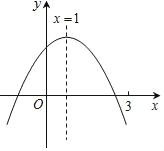
A. 2 B. 3 C. 4 D. 5
相关试题
