【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④方程ax2+bc+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
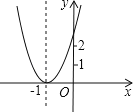
A.2 B.3 C.4 D.5
参考答案:
【答案】C
【解析】
试题分析:①首先根据抛物线开口向上,可得a>0;然后根据对称轴在y轴左边,可得b>0;最后根据抛物线与y轴的交点在x轴的上方,可得c>0,据此判断出abc>0即可.
②根据二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,可得△=0,即b2﹣4a(c+2)=0,b2﹣4ac=8a>0,据此解答即可.
③首先根据对称轴x=﹣![]() =﹣1,可得b=2a,然后根据b2﹣4ac=8a,确定出a的取值范围即可.
=﹣1,可得b=2a,然后根据b2﹣4ac=8a,确定出a的取值范围即可.
④根据顶点为(﹣1,0),可得方程ax2+bc+c=﹣2的有两个相等实根,
⑤根据点BC在对称轴右侧,y随x的增大而增大来判断即可.
解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c+2>2,
∴c>0,
∴abc>0,
∴结论①正确;
∵二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,
∴△=0,
即b2﹣4a(c+2)=0,
∴b2﹣4ac=8a>0,
∴结论②不正确;
∵对称轴x=﹣![]() =﹣1,
=﹣1,
∴b=2a,
∵b2﹣4ac=8a,
∴4a2﹣4ac=8a,
∴a=c+2,
∵c>0,
∴a>2,
∴结论③正确;
∵二次函数y=ax2+bx+c+2的顶点为(﹣1,0),
∴方程ax2+bx+c+2=0的根为x1=x2=﹣1;
∴结论④正确;
∵x>﹣1,y随x的增大而增大,
∴y1>y2,
∴结论⑤正确.
综上,可得正确结论的个数是2个:①③④⑤.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
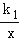 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).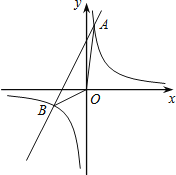
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=
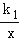 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一正数a的两个平方根分别是2m-3和5-m,求a的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AC=BC,∠ACB=90゜,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90゜得线段BN,AN交直线BC于M.
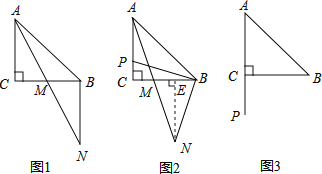
(1)如图1.若点P与点C重合,则
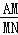 = ,
= ,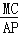 = (直接写出结果):
= (直接写出结果):(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出
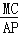 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过A (1,0)、B(0,3)及C(3,0)点,动点D从原点O开始沿OB方向以每秒1个单位长度移动,动点E从点C开始沿CO方向以每秒1个长度单位移动,动点D、E同时出发,当动点E到达原点O时,点D、E停止运动.
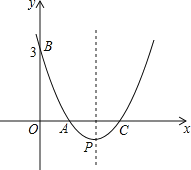
(1)求抛物线的解析式及顶点P的坐标;
(2)若F(﹣1,0),求△DEF的面积S与E点运动时间t的函数解析式;当t为何值时,△DEF的面积最大?最大面积是多少?
(3)当△DEF的面积最大时,抛物线的对称轴上是否存在一点N,使△EBN是直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠B=50°,CM是∠BCD的平分线,CM⊥CN,求∠ECN的度数.
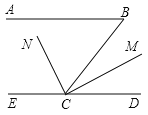
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )
A. 9 cm B. 12 cm C. 9 cm或12 cm D. 14 cm
相关试题

