搜索
【题目】先观察下列各式，再解答后面问题：
＝x2+11x+30；
＝x2﹣11x+30；
＝x2+x﹣30；
＝x2﹣x﹣30；
（1）根据以上各式呈现的规律，用公式表示出来，则
＝ ；
（2）试用你写的公式，直接写出下列两式的结果
①
＝ ；
②
＝ ．
参考答案：
【答案】（1）x2+(m+n)x+mn；（2）①a2﹣a﹣9900；②y2﹣13y+40
【解析】
（1）直接利用已知中运算规律得出答案；
（2）①结合已知运算规律即可得出答案；
②结合已知运算规律即可得出答案．
（1）（x+m）（x+n）＝x2+（m+n）x+mn；
故答案为：x2+（m+n）x+mn；
（2）①（a+99）（a﹣100）＝a2﹣a﹣9900；
②（y﹣5）（y﹣8）＝y2﹣13y+40．
故答案为：a2﹣a﹣9900；y2﹣13y+40．
-
科目： 来源： 题型：
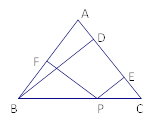
查看答案和解析>>【题目】如图，在△ABC中,AB=AC,P为BC边上任意一点,PF⊥AB于F,PE⊥AC于E,若AC边上的高BD=a.
(1)试说明PE＋PF=a;
(2)若点P在BC的延长线上,其它条件不变,上述结论还成立吗?如果成立请说明理由;如果不成立,请重新给出一个关于PE,PF,a的关系式,不需要说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示双曲线y=
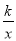与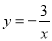
分别位于第三象限和第二象限,A是y轴上任意一点,B是
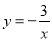上的点,C是y=
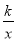上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法：①双曲线y=
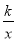在每个象限内,y随x的增大而减小；②若点B的横坐标为-3,则C点的坐标为(-3, 
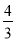)；③k=4；④△ABC的面积为定值7.正确的有（ ）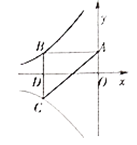
A. I个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上
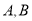两点开始时所对应的数分别是
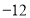和6.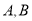两点各自以一定的速度在数轴上运动，且
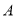点的运动速度为2个单位长度∕秒.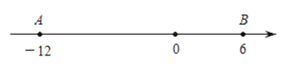
（1）若点
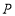为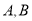两点初始时线段
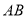的中点，则点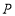所表示的数是_____；（2）
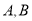两点同时出发相向而行，在原点处相遇，求
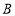点的运动速度；（3）若
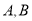两点按（2）中的速度同时出发，向数轴正方向运动，几秒时两点相距6个单位长度？ -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料，完成任务：
自相似图形
定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．
任务：
（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为 ；
（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为 ；
（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．
请从下列A、B两题中任选一条作答：我选择 题．
A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a= （用含b的式子表示）；
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a= （用含n，b的式子表示）；
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a= （用含b的式子表示）；
②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a= （用含m，n，b的式子表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为（ ）
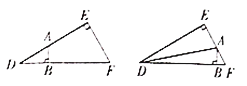
A. （A） B. （B） C. （C） D. （D）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设
=y，求y关于x的函数关系式，并写出它的定义域；（3）当∠ABE的正切值是
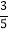时，求AB的长．
相关试题
