【题目】如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).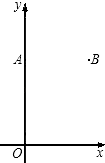
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
①点P到A,B两点的距离相等;
②点P到∠xOy的两边的距离相等.
(2)在(1)作出点P后,写出点P的坐标.
参考答案:
【答案】
(1)解:作图如右,点P即为所求作的点.
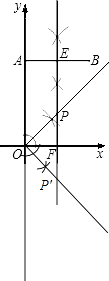
(2)解:设AB的中垂线交AB于E,交x轴于F,
由作图可得,EF⊥AB,EF⊥x轴,且OF=3,
∵OP是坐标轴的角平分线,
∴P(3,3),
同理可得:P(3,﹣3),
综上所述:符合题意的点的坐标为:(3,3),(3,﹣3).
【解析】(1)作出AB的中垂线及∠xOy的平分线,两线的交点就是所求的点;
(2)设AB的中垂线交AB于E,交x轴于F,由作图可得,EF⊥AB,EF⊥x轴,且OF=3,根据一象限角平分线上的点横纵坐标相同得出P(3,3),再根据四象限角平分线上的点横纵坐标互为相反数得出P(3,﹣3),
【考点精析】根据题目的已知条件,利用角平分线的性质定理和线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题.
(1)不改变分式的值,把下列分子和分母的最高次的系数都化为正数
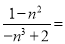 ________.
________.(2)不改变分式的值,把下列分子和分母的中各项系数都化为整数
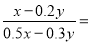 ________.
________.(3)若分式
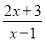 的值是整数,求整数
的值是整数,求整数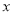 的值.
的值.(4)已知
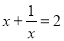 ,求
,求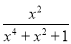 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
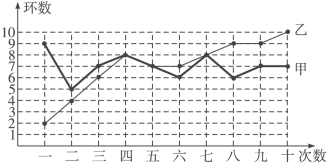
(1)请填写下表:
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
1
乙
5.4
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
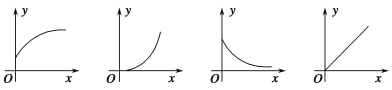
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).
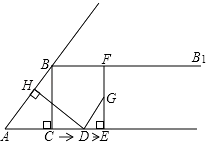
(1)当t为时,AD=AB,此时DE的长度为;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>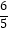 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
③当线段A′C′与射线BB1有公共点时,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2018按一定规律排列如下表:
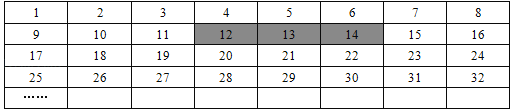
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2019 B. 2018 C. 2016 D. 2013
相关试题

