【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
参考答案:
【答案】
(1)解:由图表数据观察可知y1与t之间是二次函数关系,
设y1=a(t﹣0)(t﹣30)
再代入t=5,y1=25可得:
a=﹣ ![]()
∴y1=﹣ ![]() t(t﹣30)(0≤t≤30)
t(t﹣30)(0≤t≤30)
(2)解:由函数图象可知y2与t之间是分段的一次函数由图象可知:
0≤t<20时,y2=2t,当20≤t≤30时,y2=﹣4t+120,
∴y2= ![]()
(3)解:当0≤t<20时,y=y1+y2=﹣ ![]() t(t﹣30)+2t=80﹣
t(t﹣30)+2t=80﹣ ![]() (t﹣20)2,
(t﹣20)2,
可知抛物线开口向下,t的取值范围在对称轴左侧,y随t的增大而增大,所以最大值小于当t=20时的值80,
当20≤t≤30时,y=y1+y2=﹣ ![]() t(t﹣30)﹣4t+120=125﹣
t(t﹣30)﹣4t+120=125﹣ ![]() (t﹣5)2,
(t﹣5)2,
可知抛物线开口向下,t的取值范围在对称轴右侧,y随t的增大而减小,所以最大值为当t=20时的值80,
故上市第20天,国内、外市场的日销售总量y最大,最大值为80万件.
【解析】(1)从表中可以看出,y 随着t的增大,先增后减,不会是一次函数,就是二次函数;(2)分段函数以t=20为分界点,利用待定系数法,分别设出解析式,求出解析式;(3)由y2是分段函数,因此y与t也是分段函数,分别求出0≤t<20与20≤t≤30的关系式,在自变量的取值范围内求出最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境
(1)如图①,已知
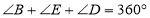 ,试探究直线
,试探究直线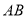 与
与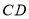 有怎样的位置关系?并说明理由.
有怎样的位置关系?并说明理由.小明给出下面正确的解法:
直线
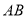 与
与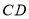 的位置关系是
的位置关系是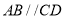 .
.理由如下:
过点
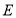 作
作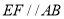 (如图②所示)
(如图②所示)所以
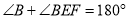 (依据1)
(依据1)因为
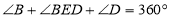 (已知)
(已知)所以
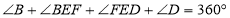
所以
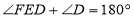
所以
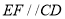 (依据2)
(依据2)因为
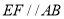
所以
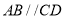 (依据3)
(依据3)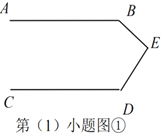
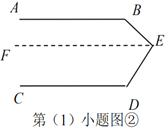
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:________________________________;
“依据2”:________________________________;
“依据3”:________________________________.
类比探究
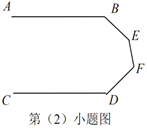
(2)如图,当
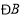 、
、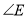 、
、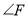 、
、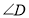 满足条件________时,有
满足条件________时,有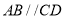 .
.拓展延伸
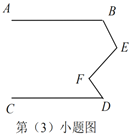
(3)如图,当
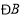 、
、 、
、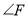 、
、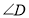 满足条件_________时,有
满足条件_________时,有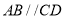 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题.
(1)不改变分式的值,把下列分子和分母的最高次的系数都化为正数
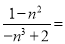 ________.
________.(2)不改变分式的值,把下列分子和分母的中各项系数都化为整数
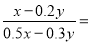 ________.
________.(3)若分式
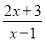 的值是整数,求整数
的值是整数,求整数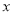 的值.
的值.(4)已知
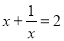 ,求
,求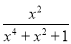 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
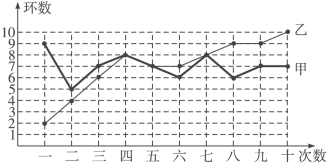
(1)请填写下表:
平均数
方差
中位数
命中9环及以上的次数
甲
7
1.2
1
乙
5.4
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
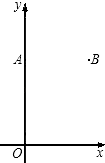
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
①点P到A,B两点的距离相等;
②点P到∠xOy的两边的距离相等.
(2)在(1)作出点P后,写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
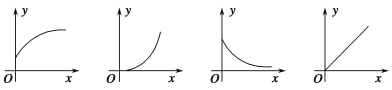
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).
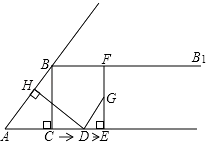
(1)当t为时,AD=AB,此时DE的长度为;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>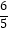 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
③当线段A′C′与射线BB1有公共点时,求t的取值范围.
相关试题

