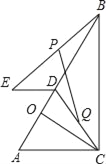
【题目】如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q.
(1)求AO的长;
(2)求PQ的长;
(3)设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.
参考答案:
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析: (1)由△ABC∽△ACO,得![]() =
=![]() ,由此即可求出OA.
,由此即可求出OA.
(2)如图2中,取BD中点F,CD中点Q,连接PF、QF,在Rt△PFQ中,求出PF,QF即可解决问题.
(3)如图3中,取AD中点G,连接GQ,由PF∥GQ,推出△PMF∽△QMG,推出![]() =
=![]() =
=![]() ,由PM+QM=
,由PM+QM=![]() ,可以求出PM,QM,即可解决问题.
,可以求出PM,QM,即可解决问题.
试题解析:
解:(1)如图1中,
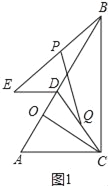
∵CO⊥AB,
∴∠AOC=∠ACB=90°,∵∠A=∠A,
∴△ABC∽△ACO,
∴![]() =
=![]() ,
,
∵AB=![]() =
=![]() =13,
=13,
∴OA=![]() =
=![]() .
.
(2)如图2中,取BD中点F,CD中点Q,连接PF、QF,
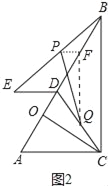
则PF∥ED,FQ∥BC,PF⊥FQ,且PF=![]() ED=1,FQ=
ED=1,FQ=![]() BC=6,
BC=6,
在Rt△PFQ中,PQ=![]() =
=![]() =
=![]() .
.
(3)如图3中,取AD中点G,连接GQ,
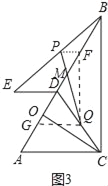
∵GQ∥AC,ED∥AC,PF∥ED,
∴PF∥GQ,
∴△PMF∽△QMG,
∴![]() =
=![]() =
=![]() ,
,
∵PM+QM=![]() ,
,
∴PM=![]() ,MQ=
,MQ=![]() ,
,
∴|PM﹣QM|=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )
A.﹣1
B.1
C.﹣4
D.4 -
科目: 来源: 题型:
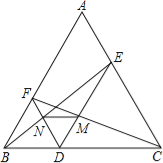
查看答案和解析>>【题目】如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
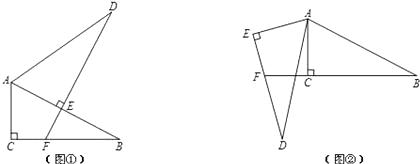
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由. -
科目: 来源: 题型:
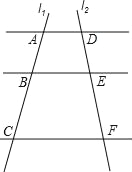
查看答案和解析>>【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,
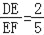 ,AC=14;
,AC=14;(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
-
科目: 来源: 题型:
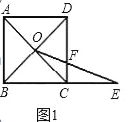
查看答案和解析>>【题目】数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
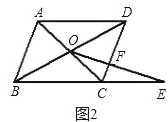
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
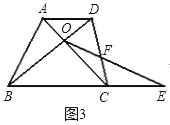
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求式子中x的值:4(x﹣1)2﹣16=0.
相关试题

