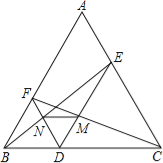
【题目】如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
参考答案:
【答案】△DMN为等边三角形,理由见解析.
【解析】试题分析:由已知可得△BDF、△EDC是等边三角形,从而可证△BDE≌△FDC,继而可证△NDE≌△MDC,从而问题得以解决.
试题解析:△DMN为等边三角形,理由如下:
∵△ABC为等边三角形,∴∠ACB=∠ABC=60°,∵DE//AB,DF∥AC,∴∠EDC=∠ABC=60°,∠FDB=∠ACB=60°,∴∠FDE=60°,△BDF、△EDC是等边三角形,∴BD=FD,ED=CD,∵∠BDE=∠FDC=120°,∴△BDE≌△FDC,∴∠BED=∠FCD,又∵∠NDE=∠MDC=60°,∴△NDE≌△MDC,∴DN=DM,∴△DMN是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则
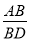 的值为( )
的值为( )
A.
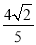 B.
B. 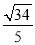 C.
C. 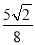 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )
A.﹣1
B.1
C.﹣4
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
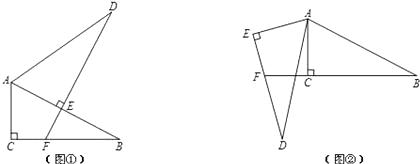
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由. -
科目: 来源: 题型:
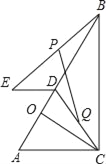
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q.
(1)求AO的长;
(2)求PQ的长;
(3)设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,
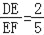 ,AC=14;
,AC=14;(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
相关试题

