【题目】如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
参考答案:
【答案】
(1)
解:当y=0时,﹣3x﹣3=0,x=﹣1
∴A(﹣1,0)
当x=0时,y=﹣3,
∴C(0,﹣3),
∴ ![]()
∴ ![]() ,
,
抛物线的解析式是:y=x2﹣2x﹣3.
当y=0时,x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3
∴B(3,0)
(2)
解:由(1)知B(3,0),C(0,﹣3)直线BC的解析式是:y=x﹣3,
设M(x,x﹣3)(0≤x≤3),则E(x,x2﹣2x﹣3)
∴ME=(x﹣3)﹣(x2﹣2x﹣3)=﹣x2+3x=﹣(x﹣ ![]() )2+
)2+ ![]() ;
;
∴当x= ![]() 时,ME的最大值为
时,ME的最大值为 ![]()
(3)
解:答:不存在.
由(2)知ME取最大值时ME= ![]() ,E(
,E( ![]() ,﹣
,﹣ ![]() ),M(
),M( ![]() ,﹣
,﹣ ![]() )
)
∴MF= ![]() ,BF=OB﹣OF=
,BF=OB﹣OF= ![]() .
.
设在抛物线x轴下方存在点P,使以P、M、F、B为顶点的四边形是平行四边形,
则BP∥MF,BF∥PM.
∴P1(0,﹣ ![]() )或P2(3,﹣
)或P2(3,﹣ ![]() )
)
当P1(0,﹣ ![]() )时,由(1)知y=x2﹣2x﹣3=﹣3≠﹣
)时,由(1)知y=x2﹣2x﹣3=﹣3≠﹣ ![]()
∴P1不在抛物线上.
当P2(3,﹣ ![]() )时,由(1)知y=x2﹣2x﹣3=0≠﹣
)时,由(1)知y=x2﹣2x﹣3=0≠﹣ ![]()
∴P2不在抛物线上.
综上所述:在x轴下方抛物线上不存在点P,使以P、M、F、B为顶点的四边形是平行四边形
【解析】(1)先根据直线的解析式求出A、C两点的坐标,然后将A、C的坐标代入抛物线中即可求出二次函数的解析式.进而可根据抛物线的解析式求出B点的坐标.(2)ME的长实际是直线BC的函数值与抛物线的函数值的差,据此可得出一个关于ME的长和F点横坐标的函数关系式,可根据函数的性质来求出ME的最大值.(3)根据(2)的结果可确定出F,M的坐标,要使以M,F,B,P为顶点的四边形是平行四边形,必须满足的条件是MP∥=BF,那么只需将M点的坐标向左或向右平移BF长个单位即可得出P点的坐标,然后将得出的P点坐标代入抛物线的解析式中,即可判断出是否存在符合条件的P点.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
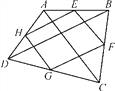
查看答案和解析>>【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
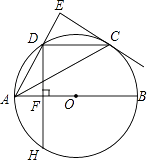
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a=2016×2018-2016×2017, b=2015×2016-2013×2017,
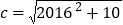 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )A. a<b<c B. a<c<b C. b<a<c D. b<c<a
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,且a≠0,b≠0,a+b≠0,则函数y=ax+b与
 在同一坐标系中的图像不可能是( )
在同一坐标系中的图像不可能是( )
A.
B.
C.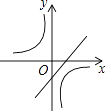
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十·一”黄金周期间,我市某景点旅游区在7天假期中每天旅游的人数变化如下表:
(正数表示比前一天多的人数,负数表示比前一天少的人数).(单位:万人)
日 期
1日
2日
3日
4日
5日
6日
7日
人数变化
+ 1.2
+ 1.2
+ 0.4
– 0.2
– 0.8
+ 0.2
– 1.4
若9月30日的旅游人数记为3万人,则
(1)请求出10月5日的旅游人数;
(2)请判断7天内旅游人数最多的是哪一天?最少的是哪一天?它们相差多少万人?
(3)若该景点门票为每人20元,请算出该景点黄金周期间的收入共多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
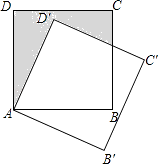
A.
B.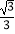
C.1﹣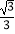
D.1﹣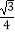
相关试题

