【题目】“十·一”黄金周期间,我市某景点旅游区在7天假期中每天旅游的人数变化如下表:
(正数表示比前一天多的人数,负数表示比前一天少的人数).(单位:万人)
日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 | + 1.2 | + 1.2 | + 0.4 | – 0.2 | – 0.8 | + 0.2 | – 1.4 |
若9月30日的旅游人数记为3万人,则
(1)请求出10月5日的旅游人数;
(2)请判断7天内旅游人数最多的是哪一天?最少的是哪一天?它们相差多少万人?
(3)若该景点门票为每人20元,请算出该景点黄金周期间的收入共多少万元?
参考答案:
【答案】4.8万
【解析】
解:(1)![]() (万人)
(万人)
答:10月5日的游客人数为4.8万人。············································· 1分
(2) 1日:![]() (万人) 2日:4.2 + 1.2 = 5.4(万人)
(万人) 2日:4.2 + 1.2 = 5.4(万人)
3日:5.4 + 0.4 = 5.8(万人) 4日:5.8 – 0.2 = 5.6(万人)
5日:5.6 – 0.8 = 4.8(万人) 6日:4.8 + 0.2 = 5(万人)
7日:5 – 1.4 = 3.6(万人)
相差:5.8 – 3.6 = 2.2(万人)
答:7天内游客人数最多的是3日,最少的是7日,它们相差2.2万人。····· 4分
(3)![]() (万元)
(万元)
答:该景点黄金周期间的收入共688万元。······································· 6分
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=2016×2018-2016×2017, b=2015×2016-2013×2017,
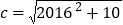 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )A. a<b<c B. a<c<b C. b<a<c D. b<c<a
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,且a≠0,b≠0,a+b≠0,则函数y=ax+b与
 在同一坐标系中的图像不可能是( )
在同一坐标系中的图像不可能是( )
A.
B.
C.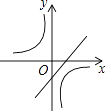
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
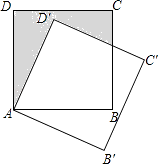
A.
B.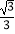
C.1﹣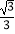
D.1﹣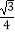
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)
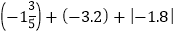
(3)

(4)[ 2
 - (
- ( )×24 ]÷5×(- 1)2001
)×24 ]÷5×(- 1)2001(5)

(6) -22 -(-1)2001×(
 -
-  )÷
)÷ +(-3)2
+(-3)2
相关试题

