搜索
【题目】如图，直线l1：y=﹣x+b与直线l2：y=kx+1相交于点A（1，3）．
（1）求直线l1、l2的函数表达式；
（2）求直线l1、l2和x轴围成的三角形ABC的面积；
（3）求直线l1、l2与坐标轴围成的四边形ABOD的面积．
参考答案：
【答案】（1）l1：y=﹣x+4，l2：y=2x+1，（2）
；（3）
.
【解析】
(1) A（1，3）分别代入y=﹣x+b与直线y=kx+1，求出k.b可得解析式；
（2）求出点B、C的坐标，再求三角形面积；
（3）先求出D、E的坐标，再根据S四边形ABOD=S△BOE﹣S△ADE，可得结果.
解：（1）∵直线l1：y=﹣x+b，经过点A（1，3）
∴3=﹣1+b，
∴b=4
∴l1：y=﹣x+4，
∵直线l2：y=kx+1，经过点（1，3）
∴3=k+1，
∴k=2
∴l2：y=2x+1，
（2）在y=﹣x+4中令y=0，x=4，
在y=2x+1中令y=0，x=
，
∴S△ABC=
×3=
，
（3）在y=﹣x+4中令x=0，y=4
在y=2x+1中令x=0，y=1，
∴S△BOE=
×4×4=8，
S△ADE=×3×1=
，
∴S四边形ABOD=S△BOE﹣S△ADE
=8﹣
=
．
-
科目： 来源： 题型：
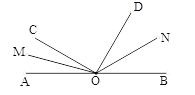
查看答案和解析>>【题目】如图所示，∠AOB是平角，OM、ON分别是∠AOC、∠BOD 的平分线．
（1）知∠AOC=40°，∠BOD=60°，求∠MON的度数；
（2）知∠COD=90°，求出∠MON的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学在安全工作月中，进行了“防自然灾害﹣地震知识知多少”专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，花粉等级后的数据整理如下表：
等级
非常了解
比较了解
基本了解
不太了解
频数
40
120
n
4
频率
0.2
m
0.18
0.02
（1）表中m的值为 ， n的值为；
（2）根据表中的数据，请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数，并补全扇形统计图；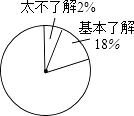
（3）若校一共有2400名学生，请根据调查结果估计全校学生中“比较了解”的人数为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题． 随着人们环保意识的增强及科学技术的进步，各种绿色环保新产品进入千家万户，今年一月份小楠家将天然气热水器换成了太阳能热水器，减少天然气的用量，去年12月份小楠家的天然气费一共是96元，从今年一月份起天然气费价格每立方米上涨了25%，小楠家2月份的用气量比去年12月份少10立方米，2月份的天然气费一共是90元，请你求小楠家今年2月份用气量是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两名同学进行登山比赛，图中表示甲、乙两人沿相同的路线同时从山脚出发，各自离山脚的距离随时间变化的图象，根据图象中的有关数据回答下列问题：
（1）分别求出表示甲、乙两同学登山过程中离山脚的距离h（千米）与时间t（时）的函数表达式；
（2）当甲到达山顶时，乙行进到山路上的某点A处，求A点距山顶的距离；
（3）在（2）的条件下，设乙同学从A点继续登山，甲同学到达山顶后游玩
小时，沿原路下山，在点B处与乙同学相遇，此时点B与山顶距离为1千米，相遇后甲、乙各自沿原路下山和上山，求乙到达山顶时，甲离山脚的距离是多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+bx+c与y轴交于点C，与x轴交于A、B两点（点A在原点左侧，点B在原点右侧），且∠ACB=90°，tan∠BAC= ． ①求抛物线的解析式；
②若抛物线顶点为P，求四边形APCB的面积．
-
科目： 来源： 题型：
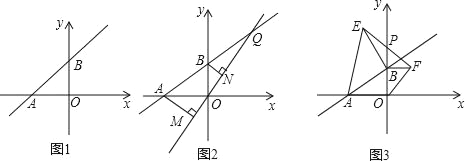
查看答案和解析>>【题目】如图1，直线l：y=mx+10m与x轴负半轴、y轴正半轴分别交于A、B两点．
（1）当OA=OB时，试确定直线l的函数表达式；
（2）在（1）的条件下，如图2，设Q为直线AB上一点，作直线OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=8，BN=6，求MN的长；
（3）当m取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图3．问：当点B在 y轴正半轴上运动时，试猜想PB的长是否为定值？若是，请求出其值；若不是，说明理由．
相关试题
