搜索
【题目】甲、乙两人参加某体育训练项目，近期的五次测试成绩得分情况如图．
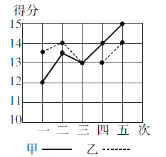
（1）分别求出两人得分的平均数与方差；
（2）根据图和上面算得的结果，对两人的训练成绩作出评价．
参考答案：
【答案】（1）甲的平均数为13.5分，方差为1；乙的平均数为13.5分，方差为0.2;(2) 乙的成绩较稳定，但甲的潜力大.
【解析】
（1）由折线图列出甲、乙近期的五次测试成绩得分，由此能求出两人得分的平均数与方差．（2）甲、乙二人的平均成绩相等，但乙比甲的成绩更稳定．
解：（1）解：（Ⅰ）由折线图知甲近期的五次测试成绩得分分别为：12，13.5，13，14，15，
∴甲得分的平均数为：
=
（12+13.5+13+14+15）=13.5.
方差为：S12=[（12-13.5）2+（13.5-13.5）2+（13-13.5）2+（14-13.5）2+（15-13.5）2]=1
乙近期的五次测试成绩得分分别为：13.5, 14,13,13,14.
∴乙得分的平均数为：
=（13.5+14+13+13+14）=13.5.
方差为：S22=[（13.5-13.5）2+（14-13.5）2+（13-13.5）2+（13-13.5）2+（14-13.5）2]= 0.2.
甲的平均数为13.5分，方差为1；乙的平均数为13.5分，方差为0.2.
（2）∵=，S12> S22
∴甲、乙二人的平均成绩相等，乙的成绩较稳定，但甲的潜力大.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一组数据6，3，4，7，6，3，5，6，求：
（1）这组数据的平均数、众数、中位数；
（2）这组数据的方差和标准差.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小聪是一名非常爱钻研的七年级学生，他将4块完全一样的三角板（如图1）拼成了一个非常工整的图形（如图2），请教老师以后得知：该图形是一个正方形，并且里面的四边形也是一个正方形，为了作进一步的探究，小明将三角板的三边长用
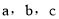表示（如图3），将两个正方形分别用正方形ABCD和正方形EFGH表示，然后他用两种不用的方法计算了正方形ABCD的面积．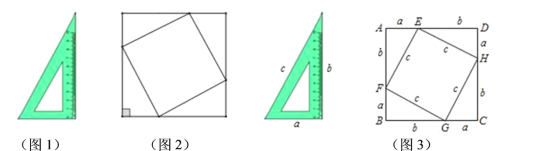
（1）请你用两种不同的方法计算出正方形ABCD的面积；
方法一： ．
方法二： ．
（2）根据（1）的计算结果，你能得到怎么样的结论？
（3）请用文字语言描述（2）中的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠C>∠B．如图①，AD⊥BC于点D，AE平分∠BAC．
（1）如图①，AD⊥BC于点D，AE平分∠BAC，能猜想出∠DAE与∠B、∠C之间的关系是什么？并说明理由．
（2）如图②，AE平分∠BAC，F为AE上的一点，且FD⊥BC于点D，这时∠EFD与∠B、∠C有何数量关系？请说明理由．
（3）如图③，AE平分∠BAC，F为AE延长线上的一点，FD⊥BC于点D，请你写出这时∠EFD与∠B、∠C之间的数量关系(只写结论，不必说明理由)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
命中环数
10
9
8
7
命中次数
3
2
（1）根据统计表（图）中提供的信息，补全统计表及扇形统计图；
（2）已知乙运动员10次射击的平均成绩为9环，方差为1．2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已如点A（1，1），B（-1，1），C（-1，-2），D（1，-2），把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处，并按
的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校举办了一次成语知识竞赛，满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀． 为了解本次大赛的成绩，校团委随机抽取了甲、乙两组学生成绩作为样本进行统计，绘制了如下统计图表：
组别
平均数
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
（1）求出表中a，b的值；
（2）小英同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上面的表格判断，小英属于哪个组？
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组． 但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你写出两条支持乙组同学观点的理由．
相关试题
