【题目】在△ABC中,∠C>∠B.如图①,AD⊥BC于点D,AE平分∠BAC.
(1)如图①,AD⊥BC于点D,AE平分∠BAC,能猜想出∠DAE与∠B、∠C之间的关系是什么?并说明理由.
(2)如图②,AE平分∠BAC,F为AE上的一点,且FD⊥BC于点D,这时∠EFD与∠B、∠C有何数量关系?请说明理由.
(3)如图③,AE平分∠BAC,F为AE延长线上的一点,FD⊥BC于点D,请你写出这时∠EFD与∠B、∠C之间的数量关系(只写结论,不必说明理由).

参考答案:
【答案】(1)![]() ,证明详见解析;(2)
,证明详见解析;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]()
【解析】
(1)由图不难发现∠EAD=∠EAC-∠DAC,再根据三角形的内角和定理及其推论结合角平分线的定义分别用结论中出现的角替换∠EAC和∠DAC.
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+![]() (∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(3)与(2)的方法相同.
证明:(1)∵AE平分∠BAC,

∴∠BAE=∠CAE=![]() ∠BAC
∠BAC
∵∠BAC=180°-(∠B+∠C)
∴∠EAC=![]() [180°-(∠B+∠C)]
[180°-(∠B+∠C)]
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∵∠EAD=∠EAC-∠DAC
∴∠EAD=![]() [180°-(∠B+∠C)]-(90°-∠C)=
[180°-(∠B+∠C)]-(90°-∠C)=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B)
(∠C-∠B)
∵AE平分∠BAC,
∴∠BAE=![]() =90°-
=90°-![]() (∠C+∠B),
(∠C+∠B),
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°-![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C)
(∠B-∠C)
∴∠EFD=![]() (∠C-∠B)
(∠C-∠B)
(3)∠EFD=![]() (∠C-∠B).
(∠C-∠B).
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C),
(∠B-∠C),
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)210+29+28+…+2+1
(2)3n+3n-1+3n-2…+3+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据6,3,4,7,6,3,5,6,求:
(1)这组数据的平均数、众数、中位数;
(2)这组数据的方差和标准差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪是一名非常爱钻研的七年级学生,他将4块完全一样的三角板(如图1)拼成了一个非常工整的图形(如图2),请教老师以后得知:该图形是一个正方形,并且里面的四边形也是一个正方形,为了作进一步的探究,小明将三角板的三边长用
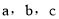 表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.
表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.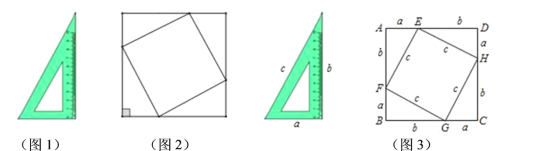
(1)请你用两种不同的方法计算出正方形ABCD的面积;
方法一: .
方法二: .
(2)根据(1)的计算结果,你能得到怎么样的结论?
(3)请用文字语言描述(2)中的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人参加某体育训练项目,近期的五次测试成绩得分情况如图.
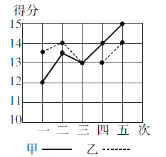
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数
10
9
8
7
命中次数
3
2
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已如点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处,并按
 的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
相关试题

