【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.

参考答案:
【答案】(1)证明见解析;(2)AE=![]() .
.
【解析】
(1)先证得OCED是平行四边形,再根据菱形的对角线互相垂直得到∠COD=90°,证得OCED是矩形,即可证明OE=CD;
(2)由菱形的性质和勾股定理求出AC与CE的长,最后根据勾股定理解答即可..
解:(1)∵在菱形ABCD中,
∴OC=![]() AC,AC⊥BD.
AC,AC⊥BD.
又∵DE:AC=1:2
∴DE=![]() AC
AC
∴DE=OC
∵DE//AC,
∴四边形OCED是平行四边形.
∵∠COD=90°
∴平行四边形OCED是矩形.
∴OE=CD
(2)∵在姜形ABCD中,
∴AB=BC=CD=AD=2,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,AO=1.
∵在矩形OCED中,CE=OD=![]()
又∵矩形DOCE中,∠OCE=90°
∴在Rt△ACE中,AE=![]() .
.
-
科目: 来源: 题型:
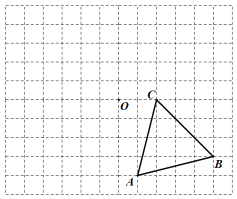
查看答案和解析>>【题目】已知△ABC的顶点A、B、C在边长为1的网格格点上.
(1)画△ABC绕点O逆时针旋转90°得到的△A1B1C1;
(2)画△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)平行四边形A1B1A2B2的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长,中华汉字,寓意深广。为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩作为样本进行整理,得到下列不完整的统计图表. 请你根据表中提供的信息,解答下列问题:
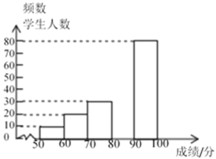
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40
(1)此次调查的样本容量为_____;
(2)在表中:
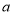 =_____,
=_____,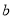 =______;
=______;(3)补全频数分布直方图;
(4)若成绩在80分以上(包括80分)的为“A”级,则该校参加这次比赛的1500名学生中,成绩为“A”级的约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.
(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学学习中,及时对知识进行归纳和整理是完善知识结构的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ .
(2)如果点C的坐标为(1,3) ,求不等式
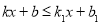 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;

图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.

图2
相关试题

