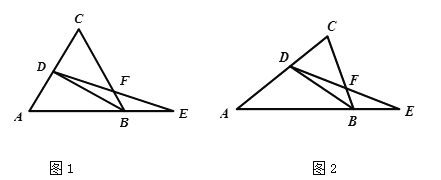
【题目】在△ABC中,AB=AC,∠ABC的平分线交AC于点D,在AB的延长线上截取BE,使BE=CD,连接DE交BC于点F.
(1)如图1,当∠CAB=60°时,若AB=2,求DE的长度;
(2)如图2,当∠CAB≠60°时,求证:BE=2BF.
参考答案:
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)如图1中,作DH⊥AB于H.在Rt△DEH中,求出DH、EH,利用勾股定理即可解决问题;
(2)如图2中,作DH∥AB交BC于H,连接EH.只要证明四边形DBEH是平行四边形,再证明BH=BE,即可解决问题.
试题解析:解:(1)如图1中,作DH⊥AB于H.
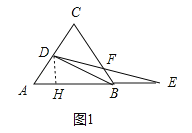
∵AC=AB,∠CAB=60°,∴△ABC是等边三角形,∴AB=BC=AC=2,∠A=60°.∵BD平分∠ABC,∴AD=DC=1.在Rt△ADH中,∵∠ADH=30°,AD=1,∴AH=![]() ,DH=
,DH=![]() .∵BE=CD=1,∴EH=BH+BE=
.∵BE=CD=1,∴EH=BH+BE=![]() .在Rt△DHE中,DE=
.在Rt△DHE中,DE=![]() =
=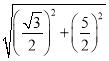 =
=![]() .
.
(2)如图2中,作DH∥AB交BC于H,连接EH.
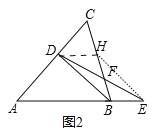
∵AB=AC,∴∠C=∠ABC.∵DH∥AB,∴∠DHC=∠ABC=∠C,∴DH=DC.∵DC=BE,∴四边形DBEH是平行四边形,∴FH=FB,BD∥EH,∴∠BHE=∠DBH,∠DBA=∠BEH.∵∠DBA=∠DBC,∴∠BHE=∠BEH,∴BH=BE,∴BE=2BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费
 自来水销售费用
自来水销售费用 污水处理费用)
污水处理费用)自来水销售价格
污水处理价格
每户每月用水量
单价:元
 吨
吨单价:元
 吨
吨17吨及以下
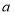
0.80
超过17吨不超过30吨的部分

0.80
超过30吨的部分
6.00
0.80
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求
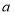 ,
, 的值.
的值.(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
-
科目: 来源: 题型:
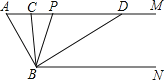
查看答案和解析>>【题目】综合与探究:如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合).BC,BD别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠ABN、∠CBD的度数;根据下列求解过程填空.
解:∵AM∥BN,
∴∠ABN+∠A=180°
∵∠A=60°,
∴∠ABN= ,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP、∠PBN= ,( )
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP= .
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在眉山市开展城乡综合治理的活动中,需要将
 、
、 、
、 三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场
三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场 、
、 两地进行处理.已知运往
两地进行处理.已知运往 地的数量比运往
地的数量比运往 地的数量的2倍少10立方米.
地的数量的2倍少10立方米.(1)求运往两地的数量各是多少立方米?
(2)若
 地运往
地运往 地
地 立方米
立方米 为整数),
为整数), 地运往
地运往 地30立方米,
地30立方米, 地运往
地运往 地的数量小于
地的数量小于 地运往
地运往 地的2倍.其余全部运往
地的2倍.其余全部运往 地,且
地,且 地运往
地运往 地不超过12立方米,则
地不超过12立方米,则 、
、 两地运往
两地运往 、
、 两地哪几种方案?
两地哪几种方案?(3)已知从
 、
、 、
、 三地把垃圾运往
三地把垃圾运往 、
、 两地处理所需费用如下表:
两地处理所需费用如下表: 地
地 地
地 地
地运往
 地(元
地(元 立方米)
立方米)22
20
20
运往
 地(元
地(元 立方米)
立方米)20
22
21
在(2)的条件下,请说明哪种方案的总费用最少?
-
科目: 来源: 题型:
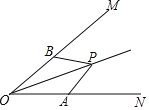
查看答案和解析>>【题目】如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

相关试题

