[题目]三角形的中线的性质:三角形的中线等分三角形的面积．面积比和线段比的联系:(1)如图1.M为△ABC的AB上一点.且BM=2AM．若△ABC的面积为a.若△CBM的面积为S.则S= (用含a的代数式表示)．(2)如图2.已知△CDE的面积为1...求△ABC的面积．(3)如图3．在△ABC中.M是AB的三等分点().N是BC的中点.若△ABC的面积是1.请直接写� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】（数学经验）三角形的中线的性质：三角形的中线等分三角形的面积．

（经验发展）面积比和线段比的联系：

（1）如图1，M为△ABC的AB上一点，且BM=2AM．若△ABC的面积为a，若△CBM的面积为S，则S=_______(用含a的代数式表示)．

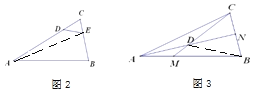
（结论应用）（2）如图2，已知△CDE的面积为1，，，求△ABC的面积．

（迁移应用）（3）如图3．在△ABC中，M是AB的三等分点()，N是BC的中点，若△ABC的面积是1，请直接写出四边形BMDN的面积为________．

【答案】（1）a（2）12（3）

【解析】

（1）根据三角形的面积公式及比例特点即可求解；

（2）连接AE，先求出△ACE的面积，再得到△ABC的面积即可；

（3）连接BD，设△ADM的面积为a，则△BDM的面积为2a,设△CDN的面积为b，则△BDN的面积为b，根据图形的特点列出方程组求出a,b,故可求解．

（1）设△ABC中BC边长的高为h，

∵BM=2AM．

∴BM=AB

∴S=BM×h=×AB×h=S△ABC=a

故答案为：a；

（2）如图2，连接AE，

∵

∴CD=AC

∴S△DCE=S△ACE=1

∴S△ACE=4，

∵

∴CE=CB

∴S△ACE=S△ABC=4

∴S△ABC=12；

（3）如图3，连接BD，设△ADM的面积为a，

∵

∴BM=2AM,BM=AB，

∴S△BDM=2S△ABM=2a, S△BCM=S△ABC=

设△CDN的面积为b，

∵N是BC的中点，

∴S△CDN=S△BDN=b，S△ABN=S△ABC=

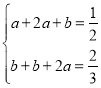∴，解得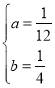

∴四边形BMDN的面积为2a+b=

故答案为．

练习册系列答案

中考新航标初中重点知识总复习指导系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，△ABC中，AB = AC，AD、AE分别是∠BAC和∠BAC外角的平分线，．

（1）求证：DA⊥AE；

（2）试判断AB与DE是否相等？并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图在平行四边形ABCD中，BC=2AB，CE⊥AB于E，F为AD的中点，若∠AEF=54，则∠B=（）

A. 54 B. 60 C. 72 D. 66

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】寒假结束了，开学后小明对本校七年级部分同学寒假阅读总时间（结果保留整10小时）进行了抽样调查，所得数据整理后制作成如图所示的频数分布直方图．观察这个频数分布直方图，给出如下结论，正确的是（）

A.小明调查了100名同学
B.所得数据的众数是40小时
C.所得数据的中位数是30小时
D.全区有七年级学生6000名，寒假阅读总时间在20小时（含20小时）以上的约有5000名