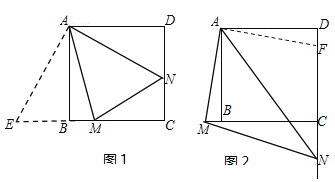
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
参考答案:
【答案】(1)BM+DN=MN成立.(2)DN-BM=MN.
【解析】试题分析:(1)、在MB的延长线上,截得BE=DN,连接AE得到△ABE≌△AND,从而得到AE=AN,然后证明△AEM≌△ANM,得到ME=MN,从而得出答案;(2)、在DC上截取DF=BM,连接AF得到△ABM≌△ADF,然后证明△MAN≌△FAN,得到所求的答案.
试题解析:(1)、BM+DN=MN成立.
如下图1,在MB的延长线上,截得BE=DN,连接AE,易证:△ABE≌△AND,∴AE=AN.
∴∠EAB=∠NMD.∴∠BAD=90°,∠NAM=45°
∴∠BAM+∠NMD=45°.∴∠EAB+∠BAM=45°.∴∠EAM=∠NAM![]() 又AM为公共边,∴△AEM≌△ANM,
又AM为公共边,∴△AEM≌△ANM,
∴ME=MN,∴ME=BE+BM=DN+BM.∴DN+BM=MN.
(2)、DN-BM=MN.
如图2,在DC上截取DF=BM,连接AF.∵AB=AD,∠ABM=∠ADF=90°,∴△ABM≌△ADF(SAS)
∴AM=AF,∠MAB=∠FAD.∴∠MAB+∠BAF=∠FAD+∠BAF=90°,即∠MAF=∠BAD=90°.
又∠MAN=45°,∴∠NAF=∠MAN=45°.∵AN=AN,∴△MAN≌△FAN.∴MN=FN,即MN=DN-DF=DN-BM;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=30°,∠A﹣∠B=30°,则∠A= .
-
科目: 来源: 题型:
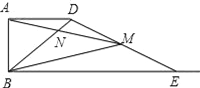
查看答案和解析>>【题目】如图,已知AB=2,AD=4,∠DAB=90°,AD∥BC.E是射线BC上的动点(点E与点B不重合),M是线段DE的中点,连结BD,交线段AM于点N,如果以A,N,D为顶点的三角形与△BME相似,则线段BE的长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 互补的角一定是邻补角B. 三角形的一个外角大于任何一个内角
C. 内错角一定相等D. 同一平面内,垂直于同一直线的两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,新华商场贴出促销海报.在商场活动期间,王莉同学随机调查了部分参与活动的顾客,并将调查结构绘制了两幅不完整的统计图.
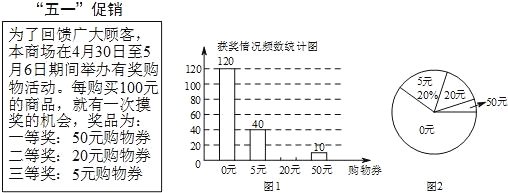
请你根据图中的信息回答下列问题:
(1)王莉同学随机调查的顾客有 人;
(2)请将统计图1补充完整;
(3)在统计图2中,“0元”部分所对应的圆心角是 度;
(4)若商场每天约有2 000人次摸奖,请估算商场一天送出的购物券总金额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的立方是它本身,那么这个数是( )
A.0
B.0或1
C.-1或1
D.0或1或-1
相关试题

