【题目】如图,一次函数y=﹣x+2的图象与反比例函数y=﹣![]() 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
(1)求A、B两点的坐标;
(2)求△ABC的面积.

参考答案:
【答案】(1)A点坐标为(﹣1,3),B点坐标为(3,﹣1);
(2)S△ABC=8.
【解析】试题分析:(1)根据反比例函数与一次函数的交点问题得到方程组,然后解方程组即可得到A、B两点的坐标;
(2)先利用x轴上点的坐标特征确定D点坐标,再利用关于y轴对称的点的坐标特征得到C点坐标,然后利用S△ABC=S△ACD+S△BCD进行计算.
试题解析:(1)根据题意得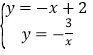 ,解方程组得
,解方程组得![]() 或
或![]() ,
,
所以A点坐标为(﹣1,3),B点坐标为(3,﹣1);
(2)把y=0代入y=﹣x+2得﹣x+2=0,解得x=2,
所以D点坐标为(2,0),
因为C、D两点关于y轴对称,
所以C点坐标为(﹣2,0),
所以S△ABC=S△ACD+S△BCD=![]() ×(2+2)×3+
×(2+2)×3+![]() ×(2+2)×1=8.
×(2+2)×1=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=
 DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=mx+n与反比例函数y=
 其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )
其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=
 ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A.
 B.
B.  +1﹣
+1﹣ C.
C.  ﹣
﹣ D.
D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S4=( )
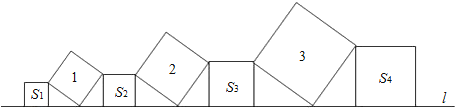
A.4B.3C.2D.1
相关试题

