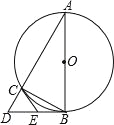
【题目】如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据弦切角定理和切线的性质可得∠CBE=∠A,∠ABD=90°,根据圆周角定理可得∠ACB=90°,即可得∠ACO+∠BCO=90°,∠BCD=90°,再由直角三角形斜边上的中线性质得出CE=![]() BD=BE,根据等腰三角形的性质可得∠BCE=∠CBE=∠A,即可证出∠ACO=∠BCE,所以∠BCE+∠BCO=90°,即CE⊥OC,所以CE是⊙O的切线;(2)由勾股定理求出AB的长,再由三角函数得出tanA=
BD=BE,根据等腰三角形的性质可得∠BCE=∠CBE=∠A,即可证出∠ACO=∠BCE,所以∠BCE+∠BCO=90°,即CE⊥OC,所以CE是⊙O的切线;(2)由勾股定理求出AB的长,再由三角函数得出tanA=![]() =
=![]() ,求出BD=
,求出BD=![]() AB=
AB=![]() ,即可得出CE的长.
,即可得出CE的长.
试题解析:(1)证明:连接OC,如图所示:
∵BD是⊙O的切线,
∴∠CBE=∠A,∠ABD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,∠BCD=90°,
∵E是BD中点,
∴CE=![]() BD=BE,
BD=BE,
∴∠BCE=∠CBE=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴∠ACO=∠BCE,
∴∠BCE+∠BCO=90°,
即∠OCE=90°,CE⊥OC,
∴CE是⊙O的切线;
(2)解:∵∠ACB=90°,
∴AB=![]() ,
,
∵tanA=![]() =
=![]() ,
,
∴BD=![]() AB=
AB=![]() ,
,
∴CE=![]() BD=
BD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足-3x>-12的非负整数有_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

-
科目: 来源: 题型:
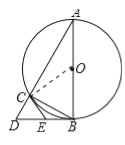
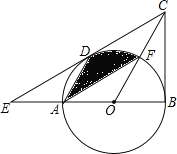
查看答案和解析>>【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m+n=-1,则(m+n)2-2m-2n的值是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个木工有两根长为40cm和60cm的木条,要另外找一根木条,钉成一个三角形木架,则第三根木条的长x的值应满足的不等式是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,点C为△ABD外接圆上的一动点(点C不在
,点C为△ABD外接圆上的一动点(点C不在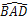 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:
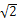 AC=BC+CD;
AC=BC+CD;(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究
 ,
, 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.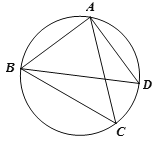
相关试题

