【题目】点![]() ,
,![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() ,
,![]() ,
,![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,在数轴上
,在数轴上![]() ,
,![]() 两点之间的距离
两点之间的距离![]() .已知数轴上
.已知数轴上![]() ,
,![]() 两点表示数
两点表示数![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() .
.
![]()
(1)![]() ,
,![]() 两点之间的距离是.
两点之间的距离是.
(2)![]() 与
与![]() 之间的距离表示为.
之间的距离表示为.
(3)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离之和为
的距离之和为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(4)现在点![]() ,点
,点![]() 分别以
分别以![]() 单位/秒和
单位/秒和![]() 单位/秒的速度同时向右运动,当点
单位/秒的速度同时向右运动,当点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度时,求点
个单位长度时,求点![]() 所对应的数是多少?
所对应的数是多少?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4)点A所对应的数是
;(4)点A所对应的数是![]() 或14.
或14.
【解析】
(1)根据绝对值的非负性求出a,b,即可得到A,B之间的距离;
(2)在数轴上A、B两点之间的距离为AB=|a-b|,依此即可求解;
(3)分两种情况:点P在点A的左边,点P在点B的右边,进行讨论即可求解;
(4)分两种情况:点A在点B的左边,点A在点B的右边,进行讨论即可求解.
(1)∵![]()
∴a=-2,b=6,
∴A点表示的数为-2,B点表示的数为6,
A,B之间的距离为![]()
(2)x与4之间的距离表示为|x(4)|=|x+4|
(3)点P在点A的左边时:16=-2-x+6-x,解得x=-6,
点P在点B的右边时:16=x-(-2)+x-6,解得x=10,
∴x的值为![]() 或
或![]() ;
;
(4)当点A在点B的左边,设运动时间为t,
(6+0.5t)-(-2+2t)=4,解得t=![]()
点A所对应的数是![]()
当点A在点B的右边,设运动时间为t,
(-2+2t) - (6+0.5t)=4,解得t=8
点A所对应的数是14
故点A所对应的数是![]() 或14.
或14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的
座位数
第2排的
座位数
第3排的
座位数
第4排的
座位数
…
a
a+2
a+4
…
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
-
科目: 来源: 题型:
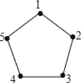
查看答案和解析>>【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了3km,到达小刚家,继续向东走了4km到达小红家,又向西走了11km到达小英家,最后回到超市。
(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴。并在数轴上表示出小刚家、小红家、小英家的位置;
(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车沿着一条南北方向的公路来回行驶.某一天早晨从A地出发,晚上到达B地.约定向北为正,向南为负,当天记录如下:(单位:千米)
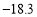 ,
,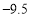 ,
,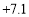 ,
,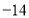 ,
,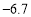 ,
,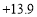 ,
,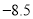
(1)问B地在A地何处,相距多少千米?
(2)若汽车行驶每千米耗油0.2升,那么这一天共耗油多少升?(精确到1升)
-
科目: 来源: 题型:
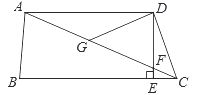
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个选项中,不是y关于x的函数的是( )
A.|y|=x﹣1 B.y=
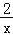 C.y=2x﹣7 D.y=x2
C.y=2x﹣7 D.y=x2
相关试题

