【题目】如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.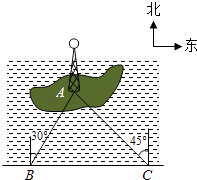
参考答案:
【答案】解:过A作AD⊥BC于D,则AD的长度就是A到岸边BC的最短距离.
在Rt△ACD中,∠ACD=45°,设AD=x,则CD=AD=x,
在Rt△ABD中,∠ABD=60°,
由tan∠ABD= ![]() ,即tan60°=
,即tan60°= ![]() ,
,
所以BD= ![]() =
= ![]() x,
x,
又BC=4,即BD+CD=4,所以 ![]() x+x=4,
x+x=4,
解得x=6﹣2 ![]() .
.
答:这个标志性建筑物底部A到岸边BC的最短距离为(6﹣2 ![]() )公里.
)公里.
【解析】过A作AD⊥BC于D,先由△ACD是等腰直角三角形,设AD=x,得出CD=AD=x,再解Rt△ABD,得出BD= ![]() =
= ![]() x,再由BD+CD=4,得出方程
x,再由BD+CD=4,得出方程 ![]() x+x=4,解方程求出x的值,即为A到岸边BC的最短距离.
x+x=4,解方程求出x的值,即为A到岸边BC的最短距离.
【考点精析】掌握等腰直角三角形是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见下表:

某居民五月份用电190千瓦时,缴纳电费90元.
(1)求x的值和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以O(0,0)、A(2,0)为顶点作正△OAP1 , 以点P1和线段P1A的中点B为顶点作正△P1BP2 , 再以点P2和线段P2B的中点C为顶点作△P2CP3 , …,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 .
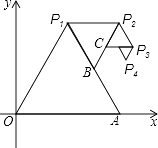
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A,B两种客车,它们的载客量和租金如下表.星星中学根据实际情况,计划用A,B型车共5辆,同时送七年级师生到校基地参加社会实践活动.

(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,请问哪种租车方案最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一种商品,单价30元,试销中发现这种商品每天的销售量夕(件)与每件的销售价
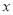 (元)满足关系:
(元)满足关系: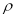 =100-2
=100-2 .若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( )
①-a一定是负数;②|-a|一定是正数;③倒数等于它本身的数是±1;
④绝对值等于它本身的数是1;⑤两个有理数的和一定大于其中每一个加数;⑥若
 ,则a=b.
,则a=b.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
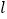 经过原点和点
经过原点和点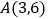 ,点
,点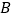 的坐标为
的坐标为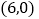 .
.(1)求直线
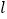 所对应的函数解析式;
所对应的函数解析式;(2)当P在线段OA上时,设
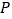 点横坐标为
点横坐标为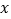 ,三角形
,三角形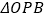 的面积为
的面积为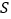 ,写出
,写出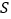 关于
关于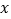 的函数解析式,并指出自变量
的函数解析式,并指出自变量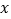 的取值范围;
的取值范围;(3)当P在射线OA上时,在坐标轴上有一点
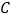 ,使
,使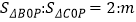 (
(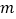 正整数),请直接写出点
正整数),请直接写出点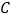 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)
相关试题

