【题目】直线![]() 经过原点和点
经过原点和点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(2)当P在线段OA上时,设![]() 点横坐标为
点横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(3)当P在射线OA上时,在坐标轴上有一点![]() ,使
,使![]() (
(![]() 正整数),请直接写出点
正整数),请直接写出点![]() 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用待定系数法即可解决问题;
(2)利用三角形的面积公式计算即可;
(3)分两种情形分别求解即可.
(1)设直线l的解析式为y=kx,
把点A坐标代入得到6=3k,
∴k=2,
∴直线l的解析式为y=2x.
(2)∵P(x,2x),B(4,0),
∴S=![]() ×4×2x=4x,(0<x≤3);
×4×2x=4x,(0<x≤3);
(3)∵点B的坐标为(6,0),点C在坐标轴上,
①当点C在x轴上时,则△BOP和△COP是同高三角形,
∵S△BOP:S△COP=2:m,
∴![]() ,
,
∴OC=3m,
∴C(3m,0)或(-3m,0);
②当点C在x轴上时,则△BOP和△COP是同高三角形,
∵P(x,2x),S△BOP:S△COP=2:m,
∴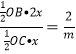 ,即
,即![]() ,
,
∴OC=6m,
∴C(0,6m)或(0,-6m).
-
科目: 来源: 题型:
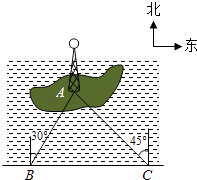
查看答案和解析>>【题目】如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一种商品,单价30元,试销中发现这种商品每天的销售量夕(件)与每件的销售价
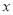 (元)满足关系:
(元)满足关系: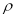 =100-2
=100-2 .若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( )
①-a一定是负数;②|-a|一定是正数;③倒数等于它本身的数是±1;
④绝对值等于它本身的数是1;⑤两个有理数的和一定大于其中每一个加数;⑥若
 ,则a=b.
,则a=b.A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣
 ,0),且与反比例函数y=
,0),且与反比例函数y=  (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B. 
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:



因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
相关试题

